题目内容

 已知等比数列{ an }中，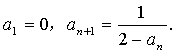

（Ⅰ）求证数列为等差数列。

（Ⅱ）设数列{an}的前n项和为Sn，证明:；

（Ⅲ）设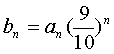，证明：对任意的正整数n、m，均有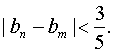

解：（1）因为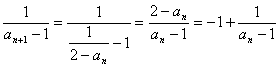

数列是以－1为首项，－1为公差的等差数列

所以

所以   ……………………4分

（2）设

则

故

所以

所以

所以

    ………………8分

（3）因为

所以

当

当

所以b1<b2<b3<b4>b5>b6>……

又因为

所以对任意的正整数n、m，均有|bn－bm|的最大值为

所以对任意的正整数n、m，均有|bn－bm|<  …………14分

练习册系列答案
相关题目
已知等比数列中{an}中，a1+a3=101，前4项和为1111，令bn=lg an，则b2009=（　　）
A、2008B、2009C、2010D、2222
已知等比数列的{an}前n项和An=(
1
3
)n-c(n∈N*，c为常数），数列{bn}（bn＞0）的首项为c，且前n项和Bn满足Bn-Bn-1=
Bn
+
Bn-1
(n≥2，n∈N*)．
（1）求常数c的值；
（2）求数列{bn}的通项公式；
（3）设数列{
1
bnbn+1
}前n项和为Tn，若对任意正整数n，
k
n
≤Tn恒成立，求实数k的最大值．
已知等比数列的{an}前n项和An=(
1
3
)n-1(n∈N*)，数列{bn}（bn＞0）的首项为1，且前n项和Bn满足
Bn
-
Bn-1
=1(n≥2，n∈N*)．
（1）求数列{an}和{bn}的通项公式；
（2）若数列{
1
bnbn+1
}前n项和为Tn，问满足Tn＞
1000
2009
的最小正整数n是多少？
已知等比数列｛an｝的前n项之和Sn=3n+a,那么a等于…(　　)

A.3             B.1                C.0                D.－1

已知等比数列｛an｝为递增数列，且，则数列｛an｝的通项公式an =______________。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网