题目内容

已知函数 $数学公式$
（1）求函数的定义域，并求 $数学公式$ 的值
（2）若-1＜a＜1，当x∈[-a，a]时，f（x）是否存在最小值，若存在，求出最小值；若不存在，请说明理由．

解：（1）由 $\text{[math]}$ 得-1＜x＜1，
∴函数f（x）的定义域是（-1，1）（3分）
∵ $\text{[math]}$ ，
∴f（x）是奇函数
∴ $\text{[math]}$ =0（3分）
（2）∵ $\text{[math]}$ 对-1＜x＜1恒成立
∴f（x）在（-1，1）上是减函数（5分）
∴ $\text{[math]}$ （3分）
分析：（1）根据使函数解析式有意义的原则，我们可以列出让函数解析式有意义的不等式，解不等式可求出函数的定义域，分析出函数奇偶性，根据奇偶性可以得到 $\text{[math]}$ 的值
（2）求出函数的导函数，可判断出函数在[-1，1]上的单调性，进而可得x∈[-a，a]时，f（x）存在最小值f（a），代入计算即可得到答案．
点评：本题考查的知识点是函数单调性的性质，函数定义域及其求法，函数奇偶性的判断，函数的值，是对函数三要素和性质比较综合的考查，掌握函数性质的定义及判断方法是解答关键．

练习册系列答案

复习计划风向标暑系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

全品中考试卷系列答案

全效系列丛书赢在期末系列答案

新天地期末系列答案

期末集结号系列答案

全优达标测试卷系列答案

中考必备6加14系列答案

相关题目

已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

）的图象和y轴交于（0，1）且y轴右侧的第一个最大值、最小值点分别为P（x₀，2）和Q（x₀+3π，-2）．
（1）求函数y=f（x）的解析式及x₀；
（2）求函数y=f（x）的单调递减区间；
（3）如果将y=f（x）图象上所有点的横坐标缩短到原来的

（纵坐标不变），然后再将所得图象沿x轴负方向平移

个单位，最后将y=f（x）图象上所有点的纵坐标缩短到原来的

（横坐标不变）得到函数y=g（x）的图象，写出函数y=g（x）的解析式并给出y=|g（x）|的对称轴方程．

已知函数f（x）=Asin（3x+φ）（ A＞0，x∈（-∞，+∞），0＜φ＜π ）在x=

时取得最大值4．
（1）求函数f（x）的最小正周期及解析式；
（2）求函数f（x）的单调增区间；
（3）求函数f（x）在[0，

]上的值域．

已知函数（1）求函数在区间[1，]上的最大值、最小值；

（2）求证：在区间（1，）上，函数图象在函数图象的下方；

（3）设函数，求证：≥。（）

（1）求函数f（x）的最小正周期和最小值；
（2）在给出的直角坐标系中，用描点法画出函数y=f（x）在区间[0，π]上的图象．

（本题满分12分）

已知函数

（1）求函数的极值点；

（2）若直线过点（0，—1），并且与曲线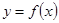相切，求直线的方程；

（3）设函数，其中，求函数在上的最小值.（其中e为自然对数的底数）