题目内容
已知中心在坐标原点焦点在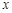 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为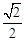 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点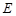 (0,1),
问是否存在直线
(0,1),
问是否存在直线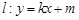 与椭圆
与椭圆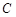 交于
交于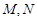 两点,且
两点,且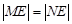 ?若存在,求出
?若存在,求出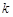 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】
(Ⅰ)  (Ⅱ) 存在这样的直线
(Ⅱ) 存在这样的直线 ,其斜率
,其斜率 的取值范围是
的取值范围是
【解析】
试题分析:(Ⅰ)由题意可设椭圆的标准方程为 1分
1分
则由长轴长等于4,即2a=4,所以a=2. 2分
又 ,所以
,所以 ,
3分
,
3分
又由于 4分
4分
所求椭圆C的标准方程为 5分
5分
(Ⅱ)假设存在这样的直线
 ,设
,设 ,
, 的中点为
的中点为
因为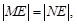 所以
所以 所以
所以 ①
①
(i)其中若 时,则
时,则 ,显然直线
,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得
,得 ,
,
 ,得
,得 ②
7分
②
7分
则 .
8分
.
8分
代入①式得,即 ,解得
,解得 11分
11分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率
,其斜率 的取值范围是
的取值范围是 13分
13分
考点:椭圆方程性质及直线与椭圆的位置关系
点评:直线与椭圆相交时常将直线与椭圆联立方程组,利用韦达定理找到根与系数的关系,进而将 转化为点的坐标表示,其中要注意条件
转化为点的坐标表示,其中要注意条件 不要忽略
不要忽略

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
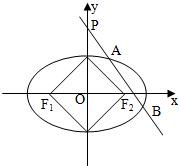 已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,
已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,
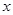 轴上,椭圆C上的点到焦点的距离的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的距离的最大值为3,最小值为1. 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.