题目内容
已知函数 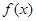 =
=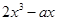 与
与 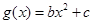 的图象都过点 P(2, 0), 且
的图象都过点 P(2, 0), 且
在点P 处有公共切线, 求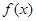 、
、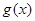 的表达式.
的表达式.
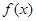 =
=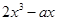 与
与 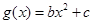 的图象都过点 P(2, 0), 且
的图象都过点 P(2, 0), 且在点P 处有公共切线, 求
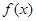 、
、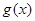 的表达式.
的表达式.f(x)=2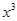 -8x, g(x)=4
-8x, g(x)=4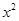 -16.
-16.
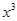 -8x, g(x)=4
-8x, g(x)=4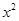 -16.
-16. 解: ∵f(x)=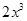 -ax 的图象过点 P(2, 0),
-ax 的图象过点 P(2, 0),
∴a=-8. …………………4分
∴f(x)=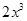 -8x …………………5分
-8x …………………5分
∴f¢(x)=6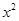 -8. …………………6分
-8. …………………6分
∵g(x)=b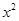 +c 的图象也过点 P(2, 0), ∴4b+c=0. ………7分
+c 的图象也过点 P(2, 0), ∴4b+c=0. ………7分
又g¢(x)=2bx, 4b=g¢(2)=f¢(2)=16 ∴b=4. ………10分
∴c=-16. ……13分
∴g(x)=4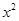 -16. 综上所述, f(x)=2
-16. 综上所述, f(x)=2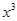 -8x, g(x)=4
-8x, g(x)=4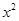 -16.
-16.
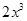 -ax 的图象过点 P(2, 0),
-ax 的图象过点 P(2, 0),∴a=-8. …………………4分
∴f(x)=
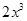 -8x …………………5分
-8x …………………5分∴f¢(x)=6
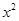 -8. …………………6分
-8. …………………6分∵g(x)=b
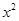 +c 的图象也过点 P(2, 0), ∴4b+c=0. ………7分
+c 的图象也过点 P(2, 0), ∴4b+c=0. ………7分又g¢(x)=2bx, 4b=g¢(2)=f¢(2)=16 ∴b=4. ………10分
∴c=-16. ……13分
∴g(x)=4
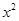 -16. 综上所述, f(x)=2
-16. 综上所述, f(x)=2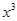 -8x, g(x)=4
-8x, g(x)=4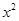 -16.
-16.
练习册系列答案
相关题目
 ,曲线
,曲线 在点(
在点( )处的
)处的
 的值;
的值;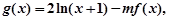 若当
若当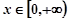 时,恒有
时,恒有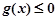 ,求
,求 的取值范围.
的取值范围.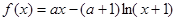
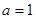 时,求
时,求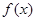 的单调区间;
的单调区间;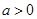 时,设
时,设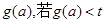 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.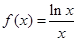 在点
在点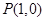 处的切线方程是 .
处的切线方程是 .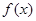 是定义在R上的奇函数,且
是定义在R上的奇函数,且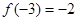 ,则
,则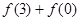 =( ).
=( ).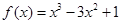 在
在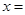 处取得极小值.
处取得极小值.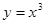 在点
在点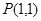 的切线方程为 .
的切线方程为 .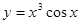 的导数是:( )
的导数是:( )



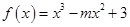 ,若
,若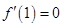 ,则
,则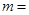 .
.