题目内容
如图所示
方格，在每一个方格中填入一个数字，数字可以是
中的任何一个，允许重复，则填入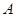
方格的数字大于
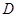方格的数字的概率为（ ）
A． | B． | C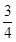． | D． |
D
解析试题分析：依题意，本题不必考虑
区域，
区域可重复填数，共有
种方法，符合
的共有
种，所以
考点：1排列组合；2古典概型概率。
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
二项式
展开式中的常数项是( )
| A．第7项 | B．第8项 | C．第9项 | D．第10项 |
若
的二项展开式中x3的系数为
，则a＝( )
| A．1 | B．2 | C．3 | D．4 |
某科室派出4名调研员到3个学校，调研该校高三复习备考近况，要求每个学校至少一名，则不同的分配方案有（ ）种
| A．144 | B．72 | C．36 | D．48 |
使
n(n∈N*)的展开式中含有常数项的最小的n为( )
| A．4 | B．5 |
| C．6 | D．7 |
现有4名教师参加说课比赛，共有4道备选题目，若每位教师从中有放回地随机选出一道题目进行说课，其中恰有一道题目没有被这4位教师选中的情况有( )
| A．288种 | B．144种 |
| C．72种 | D．36种 |
在
5的二项展开式中，x的系数为( )．
| A．10 | B．－10 | C．40 | D．－40 |
某班班会准备从含甲、乙的7人中选取4人发言，要求甲、乙两人至少有一人参加，且若甲、乙同时参加，则他们发言时顺序不能相邻，那么不同的发言顺序有( )．
| A．720种 | B．520种 | C．600种 | D．360种 |
某高校从5名男大学生志愿者和4名女大学生志愿者中选出3名派到3所学校支教(每所学校一名志愿者)，要求这3名志愿者中男、女大学生都有，则不同的选派方案共有 ( )．
| A．210种 | B．420种 |
| C．630种 | D．840种 |