Question

．（本题满分12分）如图，三棱柱ABC—A₁B₁C₁中，AA₁⊥面ABC，BC⊥AC，BC=AC=2，AA₁=3，D为AC的中点.

   （1）求证：AB₁// 面BDC₁；

　 （2）求二面角C₁—BD—C的余弦值；

   （3）在侧棱AA­₁上是否存在点P，使得

CP⊥面BDC₁？并证明你的结论.

 

 

 

 

Answer 1

【答案】

 

（I）证明：

          连接B₁C，与BC₁相交于O，连接OD

        ∵BCC₁B₁是矩形，∴O是B₁C的中点.又D是AC的中点，

∴OD//AB₁.∵AB_­1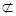面BDC_­1，OD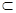面BDC₁

∴AB₁//面BDC₁.           

（II）解：如力，建立空间直角坐标系，则

         C₁（0，0，0），B（0，3，2），C（0，3，0），A（2，3，0）， D（1，3，0）

         设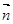=（x₁，y₁，z₁）是面BDC₁的一个法向量，则

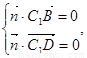即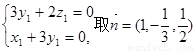.…………6分

易知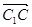=(0，3，0)是面ABC的一个法向量.

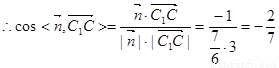∴二面角C₁—BD—C的余弦值为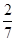 

   （III）假设侧棱AA₁上存在一点P（2，y，0）（0≤y≤3），使得CP⊥面BDC₁.

         则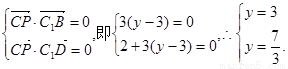

          ∴方程组无解.∴假设不成立. ∴侧棱AA₁上不存在点P，使CP⊥面BDC₁.

 

【解析】略