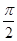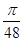题目内容
如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是 ( ) 
A. | B. | C.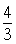 | D. |
A
解析试题分析:该几何体,是一正方体的一半---三棱柱去掉一个底面为腰长为2的等腰直角三角形,高为2的三棱锥(如图),所以结合数据,其体积为: ,故选A。
,故选A。
考点:本题主要考查三视图,几何体的体积计算。
点评:基础题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。三视图视图过程中,要注意虚线的出现,意味着有被遮掩的棱。

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
一个体积为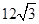 的正三棱柱的三视图,如图所示,则此正三棱柱的侧视图面积为( )
的正三棱柱的三视图,如图所示,则此正三棱柱的侧视图面积为( ) 
A.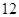 | B.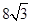 | C.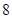 | D. |
一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
一个三棱锥的三视图如图,则该三棱锥的体积为( )
A. | B. | C. | D. |
一个棱锥的三视图如图(尺寸的长度单位为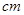 ),则该棱锥的体积是
),则该棱锥的体积是 
A. | B.8 |
| C.4 | D. |
若 ,
, 是异面直线,
是异面直线, ,
, 也是异面直线,则
也是异面直线,则 与
与 的位置关系是
的位置关系是
| A.异面 | B.相交或平行 | C.平行或异面 | D.相交或平行或异面 |
一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积
A. | B. | C.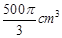 | D. |
已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中a的值为
| A.8 | B.6 |
| C.4 | D.2 |
 ·
· =0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )