题目内容
设数列{an}中的,a1=1,an-an-1=n-1(n≥2).则a6= .
【答案】分析:直接利用an-an-1=n-1(n≥2),把n=1,2,3,4,5代入,得到五个等式,相加即可求出结论.
解答:解:∵a1=1,an-an-1=n-1(n≥2).
∴a2-a1=1;
a3-a2=2
…
a6-a5=5.
把以上各式相加得:a6-a1=1+2+3+4+5=15
∴a6=a1+15=16.
故答案为:16.
点评:本题主要考查数列递推式的应用以及叠加法的应用.解决本题的关键是由an-an-1=n-1(n≥2),把n=1,2,3,4,5代入,得到五个等式,再相加求出结论.
解答:解:∵a1=1,an-an-1=n-1(n≥2).
∴a2-a1=1;
a3-a2=2
…
a6-a5=5.
把以上各式相加得:a6-a1=1+2+3+4+5=15
∴a6=a1+15=16.
故答案为:16.
点评:本题主要考查数列递推式的应用以及叠加法的应用.解决本题的关键是由an-an-1=n-1(n≥2),把n=1,2,3,4,5代入,得到五个等式,再相加求出结论.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
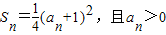 .
.