题目内容
已知函数 ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.
(Ⅰ)求 的对称中心;
的对称中心;
(Ⅱ)当 时,求
时,求 的单调增区间.
的单调增区间.
 ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.(Ⅰ)求
 的对称中心;
的对称中心;(Ⅱ)当
 时,求
时,求 的单调增区间.
的单调增区间.(Ⅰ) (Ⅱ)
(Ⅱ) ,
,
 (Ⅱ)
(Ⅱ) ,
,
试题分析:(Ⅰ)
 .
.由题意,
 ,即
,即 ,所以
,所以 ,即
,即 .
. 从而
 , 4分
, 4分令
 ,则
,则 所以对称中心为
所以对称中心为 6分
6分 (Ⅱ)
 由
由
 可得:
可得: 时
时 为单调递增函数 8分
为单调递增函数 8分
 ∴
∴ 单调递增区间为
单调递增区间为 ,
, 12分
12分点评:要考察三角函数性质先要将其整理为
 的形式,其周期性由
的形式,其周期性由 决定,对称中心是函数与x轴交点的坐标,求单调增区间时首先令
决定,对称中心是函数与x轴交点的坐标,求单调增区间时首先令 进而解不等式求x的范围
进而解不等式求x的范围
练习册系列答案
相关题目
 的最小正周期为( )
的最小正周期为( )

 个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )
个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )


 ),xÎR,则f(x)是( )
),xÎR,则f(x)是( ) 成立,则w的最小值为( )
成立,则w的最小值为( )



 ,且
,且 (
( ),设
),设 与
与 的夹角为
的夹角为
 与
与 的函数关系式;
的函数关系式; 取最大值时,求
取最大值时,求 满足的关系式.
满足的关系式.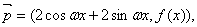
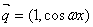 ,
,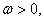
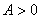 且
且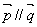 ,
,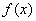 图象上相邻两条对称轴之间的距离是
图象上相邻两条对称轴之间的距离是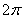 ,
,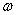 值;
值;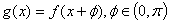 ,若
,若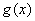 为偶函数,,求
为偶函数,,求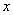 值
值 ;
; ;
; .
. 的最大值与最小值之和为
的最大值与最小值之和为