题目内容
【题目】某项科研活动共进行了5次试验，其数据如下表所示：
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
（1）从5次特征量
的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；
（2）求特征量
关于
的线性回归方程
；并预测当特征量
为570时特征量
的值.
（附：回归直线的斜率和截距的最小二乘法估计公式分别为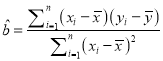
， 
）
【答案】（1）
（2）线性回归方程为
.当
时，特征量
的估计值为
.
【解析】试题分析：（1）列举出基本事件共
个，事件
的基本事件共7个，由古典概型计算公式，可得结论；（2）求出回归系数，即可求特征量
关于
的线性回归方程
，并预测当
为
时
的值.
试题解析：（1）记“至少有一个大于600”为事件
.
基本事件有
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共10个.
其中包含事件
的基本事件有
， 
， 
， 
， 
， 
， 
，共7个.
∴
.
（2）
， 
.
∴
∵
，
∴线性回归方程为
.
当
时， 
∴当
时，特征量
的估计值为
.
阅读快车系列答案【题目】当今信息时代，众多高中生也配上了手机．某校为研究经常使用手机是否对学习成绩有影响，随机抽取高三年级50名理科生的一次数学周练成绩，并制成下面的
列联表：
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 6 | 26 |
经常使用手机 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
（1）判断是否有
的把握认为经常使用手机对学习成绩有影响？
（2）从这50人中，选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙，解一道数学题，甲、乙独立解出此题的概率分别为
，且
，若
，则此二人适合结为学习上互帮互助的“学习师徒”，记
为两人中解出此题的人数，若
的数学期望
，问两人是否适合结为“学习师徒”？
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式及数据：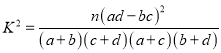 
，其中
.
【题目】为了了解某地区心肺疾病是否与性别有关，在某医院随机地对入院
的50人进行了问卷调查，得到了如下的
列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽取6人，其中男性抽多少人？
(2)在上述抽取的6人中选2人，求恰有一名女性的概率；
(3)为了研究心肺疾病是否与性别有关，请计算出统计量
，判断是否有
的把握认为
患心肺疾病与性别有关？
右面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：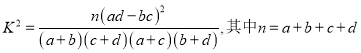 
）
