题目内容
设曲线 处的切线与直线x+ay+1=0垂直,则a=________.
处的切线与直线x+ay+1=0垂直,则a=________.
1
分析:求出函数 处的导数,即为曲线在此点的切线斜率,再利用两直线垂直的性质求出a.
处的导数,即为曲线在此点的切线斜率,再利用两直线垂直的性质求出a.
解答:y= 的导数为 y′=
的导数为 y′= ,
,
当x= 时,y′=1,
时,y′=1,
故y= 在点(
在点( ,2)处的切线斜率为1,
,2)处的切线斜率为1,
故与它垂直的直线 x+ay+1=0 的斜率为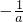 =-1,
=-1,
∴a=1,
故答案为:1.
点评:本题考查函数在某点的导数就是函数在此点的切线斜率,以及两直线垂直的性质.
分析:求出函数
 处的导数,即为曲线在此点的切线斜率,再利用两直线垂直的性质求出a.
处的导数,即为曲线在此点的切线斜率,再利用两直线垂直的性质求出a.解答:y=
 的导数为 y′=
的导数为 y′= ,
,当x=
 时,y′=1,
时,y′=1,故y=
 在点(
在点( ,2)处的切线斜率为1,
,2)处的切线斜率为1,故与它垂直的直线 x+ay+1=0 的斜率为
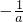 =-1,
=-1,∴a=1,
故答案为:1.
点评:本题考查函数在某点的导数就是函数在此点的切线斜率,以及两直线垂直的性质.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 处的切线与直线
处的切线与直线 _______
_______ 处的切线与直线
处的切线与直线 平行,则实数
平行,则实数 的值为 .
的值为 . 处的切线与直线x+ay+1=0垂直,则a=( )
处的切线与直线x+ay+1=0垂直,则a=( ) 处的切线与直线x+ay+1=0垂直,则a=( )
处的切线与直线x+ay+1=0垂直,则a=( )