题目内容
设x>0,y>0,z>0,a=x+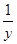 ,b=y+
,b=y+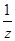 ,c=z+
,c=z+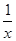 ,则a,b,c三数
,则a,b,c三数
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
C
解析试题分析:根据题意,由于x>0,y>0,z>0,a=x+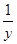 ,b=y+
,b=y+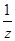 ,c=z+
,c=z+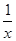 ,在可知x+
,在可知x+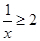 , y+
, y+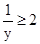 ,z+
,z+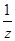
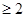 ,那么将a,bc,相加可知得到a+b+c
,那么将a,bc,相加可知得到a+b+c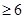 ,则可知至少有一个不小于2 ,故可知答案为C.
,则可知至少有一个不小于2 ,故可知答案为C.
考点:不等式的运用
点评:主要是考查了均值不等式求解最值的运用,属于基础题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知x>0,y>0,若 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
| A.m≥4或m≤-2 | B.m≥2或m≤-4 |
| C.-2<m<4 | D.-4<m<2 |
关于 的不等式
的不等式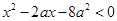 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
设集合 ,
,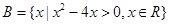 ,则
,则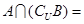 ( )
( )
A.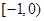 | B.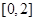 | C.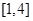 | D. |
不等式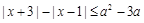 对任意实数
对任意实数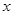 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A.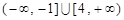 | B. |
| C.[ 1,2 ] | D. |
若不等式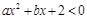 的解集为
的解集为 或
或 ,则
,则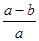 的值为( )
的值为( )
A. | B.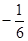 | C.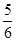 | D. |
不等式 的解集是
的解集是
A. | B. |
C.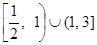 | D. |
记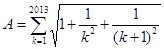 ,再记
,再记 表示不超过A的最大整数,则
表示不超过A的最大整数,则 ( )
( )
| A.2010 | B.2011 | C.2012 | D.2013 |
若关于x的不等式x2-ax-a≤-3的解集不是空集,则实数a的取值范围是( )
| A.[2,+∞) | B.(-∞,-6] |
| C.[-6,2] | D.(-∞,-6]∪[2,+∞) |