题目内容
已知![]() 试求使方程
试求使方程![]() 有解的k的取值范围。
有解的k的取值范围。
![]() .
.
解析:
解:由对数函数的性质可知,原方程的解x应满足
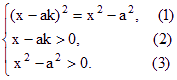
当(1),(2)同时成立时,(3)显然成立,因此只需解
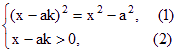
由(1)得![]()
当k=0时,由a>0知(4)无解,因而原方程无解![]()
当k≠0时,(4)的解是![]()
把(5)代入(2),得![]() ,解得:
,解得:![]()
综合得,当k在集合![]() 内取值时,原方程有解
内取值时,原方程有解![]()

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
题目内容
已知![]() 试求使方程
试求使方程![]() 有解的k的取值范围。
有解的k的取值范围。
![]() .
.
解:由对数函数的性质可知,原方程的解x应满足
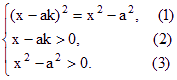
当(1),(2)同时成立时,(3)显然成立,因此只需解
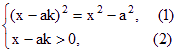
由(1)得![]()
当k=0时,由a>0知(4)无解,因而原方程无解![]()
当k≠0时,(4)的解是![]()
把(5)代入(2),得![]() ,解得:
,解得:![]()
综合得,当k在集合![]() 内取值时,原方程有解
内取值时,原方程有解![]()

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案