题目内容
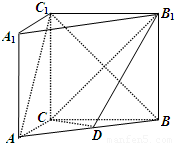
附加题(必做题)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.
(1)设
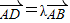 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为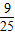 ,求λ的值;
,求λ的值;(2)若点D是AB的中点,求二面角D-CB1-B的余弦值.
【答案】分析:(1)先建立空间直角坐标系,求出各点的坐标,以及向量 ,
, 的坐标,结合
的坐标,结合 ,以及异面直线AC1与CD所成角的余弦值为
,以及异面直线AC1与CD所成角的余弦值为 ,得到关于λ的等式,即可求出结论.
,得到关于λ的等式,即可求出结论.
(2)先求两个平面法向量的坐标,再代入向量的夹角计算公式即可求出结论.
解答:解:(1)以CA,CB,CC1分别为x,y,z轴建立如图所示空间直角坐标,
因为AC=3,BC=4,AA1=4,所以A(3,0,0),B(0,4,0),C(0,0,0),C1=(0,0,4),
所以 ,因为
,因为 ,
,
所以点D(-3λ+3,4λ,0),所以 ,
,
因为异面直线AC1与CD所成角的余弦值为 ,
,
所以 ,解得
,解得 .…(4分)
.…(4分)
(2)由(1)得B1(0,4,4),因为 D是AB的中点,所以 ,
,
所以 ,
, ,平面CBB1C1的法向量
,平面CBB1C1的法向量  =(1,0,0),
=(1,0,0),
设平面DB1C的一个法向量 =(x,y,z),
=(x,y,z),
则 ,
, 的夹角(或其补角)的大小就是二面角D-CB1-B的大小,
的夹角(或其补角)的大小就是二面角D-CB1-B的大小,
由 得
得 令x=4,则y=-3,z=3,
令x=4,则y=-3,z=3,
所以 =(4,-3,3),
=(4,-3,3),
∴cos< ,
, >=
>= =
= =
= .
.
所以二面角D-B1C-B的余弦值为 . …(10分)
. …(10分)
点评:本题主要考察利用空间向量求平面间的夹角.解决这类题目的关键在于求两个平面法向量的坐标,再代入向量的夹角计算公式.
 ,
, 的坐标,结合
的坐标,结合 ,以及异面直线AC1与CD所成角的余弦值为
,以及异面直线AC1与CD所成角的余弦值为 ,得到关于λ的等式,即可求出结论.
,得到关于λ的等式,即可求出结论.(2)先求两个平面法向量的坐标,再代入向量的夹角计算公式即可求出结论.
解答:解:(1)以CA,CB,CC1分别为x,y,z轴建立如图所示空间直角坐标,
因为AC=3,BC=4,AA1=4,所以A(3,0,0),B(0,4,0),C(0,0,0),C1=(0,0,4),
所以
 ,因为
,因为 ,
,所以点D(-3λ+3,4λ,0),所以
 ,
,因为异面直线AC1与CD所成角的余弦值为
 ,
,所以
 ,解得
,解得 .…(4分)
.…(4分)(2)由(1)得B1(0,4,4),因为 D是AB的中点,所以
 ,
,所以
 ,
, ,平面CBB1C1的法向量
,平面CBB1C1的法向量  =(1,0,0),
=(1,0,0),设平面DB1C的一个法向量
 =(x,y,z),
=(x,y,z),则
 ,
, 的夹角(或其补角)的大小就是二面角D-CB1-B的大小,
的夹角(或其补角)的大小就是二面角D-CB1-B的大小,由
 得
得 令x=4,则y=-3,z=3,
令x=4,则y=-3,z=3,所以
 =(4,-3,3),
=(4,-3,3),∴cos<
 ,
, >=
>= =
= =
= .
.所以二面角D-B1C-B的余弦值为
 . …(10分)
. …(10分)点评:本题主要考察利用空间向量求平面间的夹角.解决这类题目的关键在于求两个平面法向量的坐标,再代入向量的夹角计算公式.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 附加题(必做题)
附加题(必做题) 附加题必做题如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在点P满足A1P⊥平面PBD,求实数λ的取值范围.
附加题必做题如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在点P满足A1P⊥平面PBD,求实数λ的取值范围.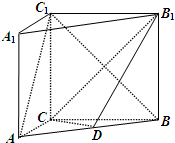
 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为 ,求λ的值;
,求λ的值;