题目内容
已知函数f(x)=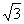
的反函数是f-1(x),则不等式f(-x)＞f-1(x)+23x的解集为A.(-1,
)∪(0,
) B.(
,0)∪(0, 
)
C.(
,0)∪(
,1) D.(-1,
)∪(
,1)
A 求得f-1(x)=f(x),且f(x)为奇函数,即f(-x)=-f(x).
∴f(-x)＞f-1 (x)+2x可整理为f(x)＜-x.
当-1＜x＜0时,＜-x,解得x∈(-1,).
当0＜x＜1时,-1＜-x,解得x∈(0, ).
综上,解集为(-1,)∪(0,
).
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知函数f(x)=2x的反函数为f-1(x)，若f-1(a)+f-1(b)=4，则
+
的最小值为（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
的图象过点A(4，
)和B（5，1）．
①求函数f（x）的解析式；②函数f（x）的反函数；③设an=log2f（n），n是正整数，是数列的前项和Sn，解关于的不等式an≤Sn．
| ax |
| b |
| 1 |
| 2 |
①求函数f（x）的解析式；②函数f（x）的反函数；③设an=log2f（n），n是正整数，是数列的前项和Sn，解关于的不等式an≤Sn．
已知函数f(x)=
的导函数为f′（x），则f′（0）=（ ）
| xex |
| cosx |
| A、0 | ||
| B、1 | ||
C、
| ||
| D、e |
已知函数f(x)=
的图象关于直线x=
对称，则f（x）的单调递增区间为（ ）
|
| π |
| 8 |
A、[kπ-
| ||||
B、[kπ-
| ||||
C、[2kπ-
| ||||
D、[2kπ-
|