Question

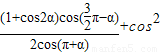设函数f（α）=α．
（1）设∠A是△ABC的内角，且为钝角，求f（A）的最小值；
（2）设∠A，∠B是锐角△ABC的内角，且∠A+∠B=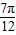，f（A）=1，BC=2，求△ABC的三个内角的大小和AC边的长．

Answer 1

【答案】分析：（1）利用诱导公式和二倍角公式对函数解析式整理，进而根据A的范围，利用正弦函数的性质求得函数的最大和最小值．
（2）利用f（A）=1求得A，进而利用∠A+∠B的值求得B，进而根据三角形内角和求得C，最后利用正弦定理求得AC．
解答：解：（1）f（A）=A=．
∵角A为钝角，
∴．
∴当2A+时，f（A）取值最小值，其最小值为．

（2）由f（A）=1得=1，∴．
∵A为锐角，∴π，
∴2A+，．
又∵A+B=，∴．∴C=．
在△ABC中，由正弦定理得：．∴．
点评：本题主要考查了三角函数的最值问题，正弦定理的应用．考查了综合分析问题的能力和基本的运算能力．