Question

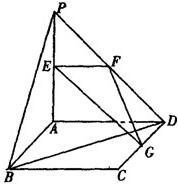如图，PA⊥平面ABCD，ABCD为正方形，，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
（1）求证：面EFG⊥面PAB；
（2）求异面直线EG与BD所成的角的余弦值；
（3）求点A到面EFG的距离．

Answer 1

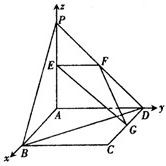解：建立如图所示的空间直角坐标系A-xyz，
则A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），
P（0，0，2），E（0，0，1），F（0，1，1），G（1，2，0）．
（1）证明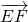：∵=（0，1，0），=（0，0，2），=（2，0，0），
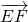∴•=0×0+1×0+0×2=0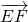，•=0×2+1×0+0×0=0，
∴EF⊥AP，EF⊥AB．
又∵AP、AB?面PAB，且PA∩AB=A，
∴EF⊥平面PAB．
又EF?面EFG，∴平面EFG⊥平面PAB．
（2）解：∵，
∴，
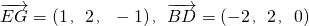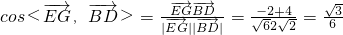（3）解：设平面EFC的法向量=（x，y，z），
则
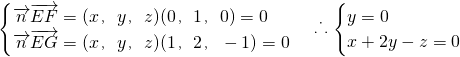
令z=0，得=（1，0，1）．
又=（0，0，1），
∴点A到平现EFG的距离．
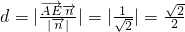分析：建系，写出有关点的坐标，A，B，C，D，P，E，F，G，（1）要证面EFG⊥面PAB，只要证EF⊥面PAB，只要证EF⊥AP，EF⊥AB即可；
（2）要求异面直线EG与BD所成的角的余弦值，只要求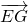与所成角的余弦值即可；（3）求出面EFG的一个法向量，求点A到面EFG的距离实际上是求向量在面EFG的法向量上的投影的长度．
点评：考查利用空间向量证明垂直和求夹角和距离问题，以及面面垂直的判定定理，体现 了转化的思想方法，属中档题．