题目内容
在平面直角坐标系中,已知 其中
其中 ,若直线
,若直线 上有且只有一点
上有且只有一点 ,使得
,使得 ,则称直线
,则称直线 为“黄金直线”,点
为“黄金直线”,点 为“黄金点”。由此定义可判断以下说法中正确的是
为“黄金点”。由此定义可判断以下说法中正确的是
①当 时,坐标平面内不存在黄金直线;
时,坐标平面内不存在黄金直线;
②当 时,坐标平面内有无数条黄金直线;
时,坐标平面内有无数条黄金直线;
③当 时,黄金点的轨迹是个椭圆;
时,黄金点的轨迹是个椭圆;
④当 时,坐标平面内有且只有一条黄金直线;
时,坐标平面内有且只有一条黄金直线;
①②③
【解析】
试题分析:根据题意,当 时,
时,
 ,就不存在这样的点
,就不存在这样的点 ,就更没有黄金直线可谈,所以①是正确的;当
,就更没有黄金直线可谈,所以①是正确的;当 时,
时, ,所以点
,所以点 的轨迹是线段
的轨迹是线段 ,所以与线段
,所以与线段 相交的直线都是黄金直线,所以有无数条,故正确;当
相交的直线都是黄金直线,所以有无数条,故正确;当 时,
时,
 ,点
,点 的轨迹是一个椭圆,对应的黄金直线都是椭圆的切线,故③是正确的;当
的轨迹是一个椭圆,对应的黄金直线都是椭圆的切线,故③是正确的;当 时,动点
时,动点 的轨迹是以原点为圆心,以5为半径的圆,黄金直线是圆的切线,有无数条,故错误,所以正确的是①②③.
的轨迹是以原点为圆心,以5为半径的圆,黄金直线是圆的切线,有无数条,故错误,所以正确的是①②③.
考点:新定义,椭圆的定义.

练习册系列答案
相关题目
 ,过点
,过点 的直线
的直线 交抛物线于A,B两点,坐标原点为O,
交抛物线于A,B两点,坐标原点为O, .
. ”是“方程
”是“方程 表示双曲线”的( )
表示双曲线”的( ) 中, 若
中, 若 , 则
, 则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 (
( )的离心率为
)的离心率为 ,且满足右焦点
,且满足右焦点 到直线
到直线 的距离为
的距离为 ,
, ,过原点且斜率为
,过原点且斜率为 的直线
的直线 与椭圆交于
与椭圆交于 两点,求
两点,求 面积的最大值。
面积的最大值。 ,若满足
,若满足 ,则
,则 解集是( )
解集是( ) B.
B.  C.
C.  D.
D. 
 ”是“方程
”是“方程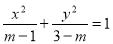 表示的曲线是焦点在
表示的曲线是焦点在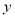 轴上的椭圆”的( )
轴上的椭圆”的( )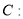
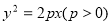 的焦点为
的焦点为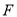 ,准线为
,准线为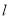 ,过抛物线上一点
,过抛物线上一点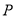 作
作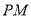 垂直
垂直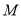 ,若
,若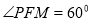 ,则
,则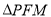 的面积为( )
的面积为( )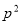 B.
B.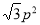 C.
C.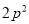 D.
D.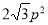
 满足等式
满足等式 ,给出下列五个关系式:
,给出下列五个关系式: ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.