题目内容
已知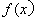 是定义在
是定义在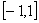 上的奇函数,且
上的奇函数,且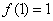 ,当
,当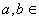
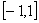 ,
,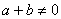 时,有
时,有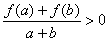 成立.
成立.
(Ⅰ)判断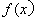 在
在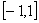 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若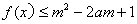 对所有的
对所有的 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
解:(Ⅰ)任取x1, x2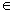 [-1, 1],且x1<x2,则-x2
[-1, 1],且x1<x2,则-x2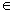 [-1, 1]. 因为f(x)为奇函数.
[-1, 1]. 因为f(x)为奇函数.
所以f(x1)-f(x2)=f(x1)+f(-x2)=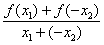 ·(x1-x2),
·(x1-x2),
由已知得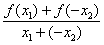 >0,x1-x2<0,
>0,x1-x2<0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2).
所以f(x)在[-1, 1]上单调递增.
(Ⅱ)因为f(1)=1, f(x)在[-1, 1]上单调递增,
所以在[-1, 1]上,f(x)≤1.
问题转化为m2-2am+1≥1,
即m2-2am≥0,对a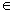 [-1, 1]恒成立.
[-1, 1]恒成立.
下面来求m的取值范围.
设g(a)=-2ma+m2≥0.
①若m=0,则g(a)=0,对a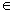 [-1, 1]恒成立。
[-1, 1]恒成立。
②若m≠0,则g(a)为a的一次函数,
若g(a)≥0,对a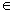 [-1, 1]恒成立,必须g(-1)≥0,且g(1)≥0,
[-1, 1]恒成立,必须g(-1)≥0,且g(1)≥0,
所以m≤-2或m≥2.
所以m的取值范围是m=0或|m|≥2.

练习册系列答案
相关题目
 的图像经过第一、三和四象限,则( )
的图像经过第一、三和四象限,则( )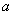 >1 B. 0<
>1 B. 0< 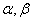 都是锐角,
都是锐角,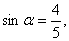
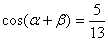 .
.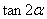 的值;
的值;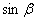 的值.
的值. ACB=
ACB= ,PA
,PA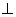 平面ABC,此图形中有 个直角三角形
平面ABC,此图形中有 个直角三角形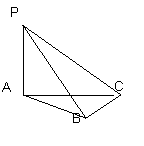
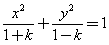 表示双曲线,则
表示双曲线,则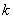 的取值范围是 ( )
的取值范围是 ( )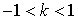 B.
B.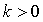 C.
C.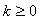 D.
D.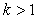 或
或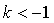
 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 .
.