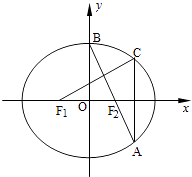题目内容
【题目】若函数![]() 满足
满足![]() 且
且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
![]() 试判断
试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
![]() 函数
函数![]() 为“
为“![]() 函数”,且当
函数”,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并写出在
的解析式,并写出在![]() 上的单调递增区间;
上的单调递增区间;
![]() 在
在![]() 条件下,当
条件下,当![]() 时,关于
时,关于![]() 的方程
的方程![]() 为常数
为常数![]() 有解,记该方程所有解的和为
有解,记该方程所有解的和为![]() ,求
,求![]() .
.
【答案】(1)不是“M函数”;(2)![]() ,
,![]() ;(3)
;(3) .
.
【解析】
![]() 由不满足
由不满足![]() ,得
,得![]() 不是“M函数”,
不是“M函数”,
![]() 可得函数
可得函数![]() 的周期
的周期![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]()
在![]() 上的单调递增区间:
上的单调递增区间:![]() ,
,![]()
![]() 由
由![]() 可得函数
可得函数![]() 在
在![]() 上的图象,根据图象可得:
上的图象,根据图象可得:
![]() 当
当![]() 或1时,
或1时,![]() 为常数
为常数![]() 有2个解,其和为
有2个解,其和为![]()
![]() 当
当![]() 时,
时,![]() 为常数
为常数![]() 有3个解,其和为
有3个解,其和为![]() .
.
![]() 当
当![]() 时,
时,![]() 为常数
为常数![]() 有4个解,其和为
有4个解,其和为![]()
即可得当![]() 时,记关于x的方程
时,记关于x的方程![]() 为常数
为常数![]() 所有解的和为
所有解的和为![]() ,
,
![]() 不是“M函数”.
不是“M函数”.
![]() ,
,![]()
![]() ,
,
![]() 不是“M函数”.
不是“M函数”.
![]() 函数
函数![]() 满足
满足![]() ,
,![]() 函数
函数![]() 的周期
的周期![]()
![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]()
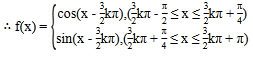 ,
,
在![]() 上的单调递增区间:
上的单调递增区间:![]() ,
,![]() ;
;
![]() 由
由![]() 可得函数
可得函数![]() 在
在![]() 上的图象为:
上的图象为:
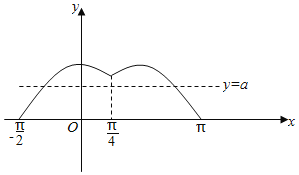
![]() 当
当![]() 或1时,
或1时,![]() 为常数
为常数![]() 有2个解,其和为
有2个解,其和为![]() .
.
![]() 当
当![]() 时,
时,![]() 为常数
为常数![]() 有3个解,其和为
有3个解,其和为![]() .
.
![]() 当
当![]() 时,
时,![]() 为常数
为常数![]() 有4个解,其和为
有4个解,其和为![]()
![]() 当
当![]() 时,记关于x的方程
时,记关于x的方程![]() 为常数
为常数![]() 所有解的和为
所有解的和为![]() ,
,
则 .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目