题目内容
求使 ≤a
≤a (x>0,y>0)恒成立的a的最小值.
(x>0,y>0)恒成立的a的最小值.
 ≤a
≤a (x>0,y>0)恒成立的a的最小值.
(x>0,y>0)恒成立的a的最小值.a的最小值是

解法一:由于a的值为正数,将已知不等式两边平方,得:
x+y+2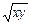 ≤a2(x+y),即2
≤a2(x+y),即2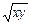 ≤(a2-1)(x+y), ①
≤(a2-1)(x+y), ①
∴x,y>0,∴x+y≥2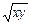 , ②
, ②
当且仅当x=y时,②中有等号成立.
比较①、②得a的最小值满足a2-1=1,
∴a2=2,a= (因a>0),∴a的最小值是
(因a>0),∴a的最小值是 .
.
解法二: 设 .
.
∵x>0,y>0,∴x+y≥2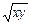 (当x=y时“=”成立),
(当x=y时“=”成立),
∴ ≤1,
≤1, 的最大值是1.
的最大值是1.
从而可知,u的最大值为 ,
,
又由已知,得a≥u,∴a的最小值为 .
.
解法三: ∵y>0,
∴原不等式可化为 +1≤a
+1≤a ,
,
设 =tanθ,θ∈(0,
=tanθ,θ∈(0,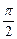 ).
).
∴tanθ+1≤a
 即tanθ+1≤asecθ
即tanθ+1≤asecθ
∴a≥sinθ+cosθ= sin(θ+
sin(θ+ ), ③
), ③
又∵sin(θ+ )的最大值为1(此时θ=
)的最大值为1(此时θ= ).
).
由③式可知a的最小值为 .
.
x+y+2
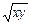 ≤a2(x+y),即2
≤a2(x+y),即2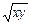 ≤(a2-1)(x+y), ①
≤(a2-1)(x+y), ①∴x,y>0,∴x+y≥2
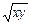 , ②
, ②当且仅当x=y时,②中有等号成立.
比较①、②得a的最小值满足a2-1=1,
∴a2=2,a=
 (因a>0),∴a的最小值是
(因a>0),∴a的最小值是 .
.解法二: 设
 .
. ∵x>0,y>0,∴x+y≥2
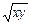 (当x=y时“=”成立),
(当x=y时“=”成立),∴
 ≤1,
≤1, 的最大值是1.
的最大值是1. 从而可知,u的最大值为
 ,
,又由已知,得a≥u,∴a的最小值为
 .
.解法三: ∵y>0,
∴原不等式可化为
 +1≤a
+1≤a ,
,设
 =tanθ,θ∈(0,
=tanθ,θ∈(0,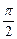 ).
).∴tanθ+1≤a

 即tanθ+1≤asecθ
即tanθ+1≤asecθ∴a≥sinθ+cosθ=
 sin(θ+
sin(θ+ ), ③
), ③又∵sin(θ+
 )的最大值为1(此时θ=
)的最大值为1(此时θ= ).
).由③式可知a的最小值为
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 则以下不等式中不恒成立的是 ( )
则以下不等式中不恒成立的是 ( ) ;
; ;
; ;
;
 的分母上的三个括号中各填入一个正整数,使得该等式成立,则所填三个正整数的和的最小值是_________
的分母上的三个括号中各填入一个正整数,使得该等式成立,则所填三个正整数的和的最小值是_________ 、
、 、
、 ,且满足
,且满足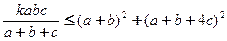 ,求
,求 的最大值。
的最大值。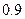 万元,年维修费用第一年是
万元,年维修费用第一年是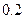 万元,以后逐年递增
万元,以后逐年递增 则
则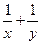 的最小值为
的最小值为  ,则在下列四个选项中,较大的是 ( )
,则在下列四个选项中,较大的是 ( )


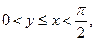 且
且 则
则 的最大值为________
的最大值为________