题目内容
已知函数  ,
, ,若不存在实数x使得
,若不存在实数x使得 同时成立,试求 a的取值范围.
同时成立,试求 a的取值范围.
解:由f(x)>1得
化简整理得
解得-2<x<-1或2<x<3
即 f(x)>1的解集为A={x|-2<x<-1或2<x<3}
由 得
得 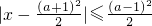
即

解得 2a≤x≤a2+1
即 的解集为B={x|2a≤x≤a2+1}
的解集为B={x|2a≤x≤a2+1}
依题意有A∩B=φ,因此有: 或2a≥3,解得:
或2a≥3,解得:
故a 的取值范围是
分析:由f(x)>1得 ,得到f(x)>1的解集为A={x|-2<x<-1或2<x<3}.由
,得到f(x)>1的解集为A={x|-2<x<-1或2<x<3}.由 得
得 的解集为B={x|2a≤x≤a2+1}.依题意有A∩B=φ,因此有:
的解集为B={x|2a≤x≤a2+1}.依题意有A∩B=φ,因此有: 或2a≥3,由此能求了a 的取值范围.
或2a≥3,由此能求了a 的取值范围.
点评:本题考查不等式有性质和应用,解题时要认真审题,注意集合的运算的灵活运用.

化简整理得

解得-2<x<-1或2<x<3
即 f(x)>1的解集为A={x|-2<x<-1或2<x<3}
由
 得
得 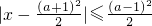
即


解得 2a≤x≤a2+1
即
 的解集为B={x|2a≤x≤a2+1}
的解集为B={x|2a≤x≤a2+1}依题意有A∩B=φ,因此有:
 或2a≥3,解得:
或2a≥3,解得:
故a 的取值范围是

分析:由f(x)>1得
 ,得到f(x)>1的解集为A={x|-2<x<-1或2<x<3}.由
,得到f(x)>1的解集为A={x|-2<x<-1或2<x<3}.由 得
得 的解集为B={x|2a≤x≤a2+1}.依题意有A∩B=φ,因此有:
的解集为B={x|2a≤x≤a2+1}.依题意有A∩B=φ,因此有: 或2a≥3,由此能求了a 的取值范围.
或2a≥3,由此能求了a 的取值范围.点评:本题考查不等式有性质和应用,解题时要认真审题,注意集合的运算的灵活运用.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
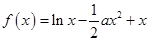 ,
, R.
R.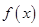 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,求
?若存在,求 是定义在
是定义在 上的奇函数,并且在
上的奇函数,并且在 上是减函数.是否存
上是减函数.是否存 使
使 恒成立?若存在,求出实数
恒成立?若存在,求出实数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
 .
.