题目内容
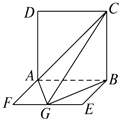
【题目】如图，在三棱柱ABC﹣A1B1C1中，面积为 
的△ACB是等腰直角三角形且∠ACB=90°，C1B⊥面ABC，C1B=3． 
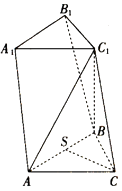
（1）若AB的中点为S，证明：CS⊥C1A．
（2）设 
，是否存在实数λ，使得直线TB与平面ACC1A1的夹角为 
？若存在，求出λ的值；若不存在，请说明理由．
【答案】
（1）证明：∵面积为 
的△ACB是等腰直角三角形且∠ACB=90°，
∴AC⊥BC，AC=BC=3，AB=3 
，
∵C1B⊥面ABC，
∴以B为原点，BC为x轴，在平面ABC中过B作AC的平行线为y轴，
BC1为z轴，建立 空间直角坐标系，
∵C1B=3，∴C（3，0，0），B（0，0，0），A（3，﹣3，0），S（ 
,- ，0），C1（0，0，3），
∴ 
=（﹣ ，﹣ ，0）， 
=（3，﹣3，﹣3），
∴ =﹣ 
=0，
∴CS⊥C1A．
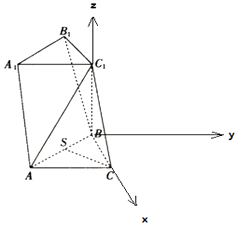
（2）解：∵ 
，∴ 
= 
，
=（0，3，0）， 
=（﹣3，3，3），
设平面ACC1A1的法向量 
=（x，y，z），
则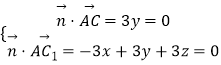 
，取x=1，得 =（1，0，1），
∵直线TB与平面ACC1A1的夹角为 
，
∴sin =|cos＜ 
＞|= 
= 
= 
，
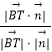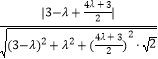解得λ= 
，不舍题意，
故不存在实数λ，使得直线TB与平面ACC1A1的夹角为 ．
【解析】（1）推导出AC⊥BC，以B为原点，BC为x轴，在平面ABC中过B作AC的平行线为y轴，BC1为z轴，建立 空间直角坐标系，利用向量法能证明CS⊥C1A．（2）求出 = ，平面ACC1A1的法向量 =（1，0，1），利用向量法推导出不存在实数λ，使得直线TB与平面ACC1A1的夹角为 ．
【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)，还要掌握空间角的异面直线所成的角(已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则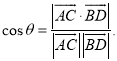
)的相关知识才是答题的关键．
