题目内容
【题目】如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= ![]() AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 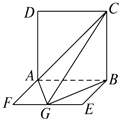
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵ABCD是正方形,∴CB⊥AB, ∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF.
∵AG,GB面ABEF,∴CB⊥AG,CB⊥BG,
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG= ![]() a,AB=2a,∴AB2=AG2+BG2 , ∴AG⊥BG,
a,AB=2a,∴AB2=AG2+BG2 , ∴AG⊥BG,
∵BG∩BC=B,∴AG⊥平面CBG,而AG面AGC,故平面AGC⊥平面BGC.
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,∴∠BGH是GB与平面AGC所成的角.
在Rt△CBG中,BH= ![]() =
= ![]() ,
,
∵BG= ![]() a,∴sin∠BGH=
a,∴sin∠BGH= ![]() =
= ![]() .
.
故选C.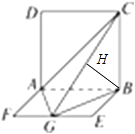
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目