题目内容
在△ABC中,若cosA=
,AB=3AC,则sinB的值为( )
| 1 |
| 3 |
A.
| B.
| C.
| D.
|
∵AB=3AC,即c=3b,
∴cosA=
=
=
,
整理得:a=2
b,
∴cosB=
=
=
,
∵B为三角形的内角,
∴sinB=
=
.
故选B
∴cosA=
| b2+c2-a2 |
| 2bc |
| b2+9b2-a2 |
| 6b2 |
| 1 |
| 3 |
整理得:a=2
| 2 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| 8b2+9b2-b2 | ||
12
|
2
| ||
| 3 |
∵B为三角形的内角,
∴sinB=
| 1-cos2B |
| 1 |
| 3 |
故选B

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
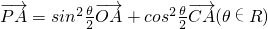 ,则
,则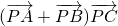 的最小值是________.
的最小值是________.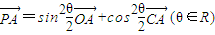 ,则
,则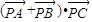 的最小值是 .
的最小值是 .