题目内容
 已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为
已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为| 16 |
| 27 |
| 16 |
| 27 |
分析:欲求所投的点落在阴影内部的概率,利用几何概型解决,只须利用定积分求出阴影图的面积,最后利用它们的面积比求得即可概率.
解答:解:由定积分可求得阴影部分的面积为
S=∫02x2dx+∫26(6-x)dx
=
x3|
+(6x-
x2)|
=
,
又Rt△AOB的面积为:
×6×6=18
所以p=
=
.
故答案为:
.
S=∫02x2dx+∫26(6-x)dx
=
| 1 |
| 3 |
2 0 |
| 1 |
| 2 |
6 2 |
=
| 32 |
| 3 |
又Rt△AOB的面积为:
| 1 |
| 2 |
所以p=
| ||
| 18 |
| 16 |
| 27 |
故答案为:
| 16 |
| 27 |
点评:本题考查了利用定积分求面积以及几何摡型知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
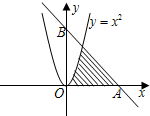 已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为________.
已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为________.