题目内容
在△ABC中,若
=-
,则cosB=______.
| cosB |
| cosC |
| b |
| 3a+c |
∵在△ABC中,
=-
,
由正弦定理得:
=
,
∴
=-
,
∴3sinAcosB+sinCcosB+sinBcosC=0,
即3sinAcosB+sin(B+C)=0,
∵在△ABC中,A+B+C=π,
∴sin(B+C)=sinA,
∴3sinAcosB+sinA=0,而sinA≠0,
∴cosB=-
.
故答案为:-
.
| cosB |
| cosC |
| b |
| 3a+c |
由正弦定理得:
| b |
| 3a+c |
| sinB |
| 3sinA+sinC |
∴
| cosB |
| cosC |
| sinB |
| 3sinA+sinC |
∴3sinAcosB+sinCcosB+sinBcosC=0,
即3sinAcosB+sin(B+C)=0,
∵在△ABC中,A+B+C=π,
∴sin(B+C)=sinA,
∴3sinAcosB+sinA=0,而sinA≠0,
∴cosB=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
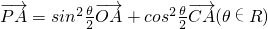 ,则
,则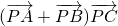 的最小值是________.
的最小值是________.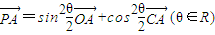 ,则
,则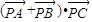 的最小值是 .
的最小值是 .