题目内容
已知数列 的各项都是正数,且对任意
的各项都是正数,且对任意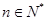 都有
都有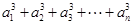
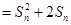 ,其中
,其中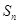 为数列
为数列 的前
的前 项和.
项和.
(1)求 、
、 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设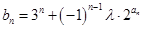 ,对任意的
,对任意的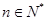 ,都有
,都有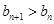 恒成立,求实数
恒成立,求实数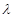 的取值范围.
的取值范围.
(1)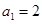 ,
,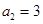 ;(2)
;(2)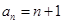 ;(3)
;(3)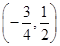 .
.
解析试题分析:(1)分别令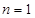 和
和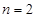 代入题干中的等式求出
代入题干中的等式求出 和
和 的值;(2)利用定义法进行求解,在原式中利用
的值;(2)利用定义法进行求解,在原式中利用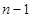 替换
替换 得到
得到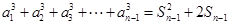 ,将此等式与原式作差得到
,将此等式与原式作差得到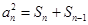
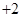 ,再次利用定义法得到数列
,再次利用定义法得到数列 为等差数列,最后利用等差数列的通项公式进行求解;(3)利用
为等差数列,最后利用等差数列的通项公式进行求解;(3)利用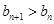 化简得到
化简得到 ,对
,对 进行分奇偶讨论求出
进行分奇偶讨论求出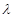 的取值范围.
的取值范围.
试题解析:(1)令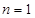 ,则
,则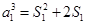 ,即
,即 ,所以
,所以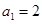 或
或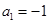 或
或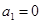 ,
,
又因为数列 的各项都是正数,所以
的各项都是正数,所以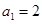 ,
,
令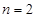 ,则
,则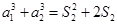 ,即
,即 ,解得
,解得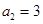 或
或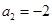 或
或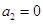 ,
,
又因为数列 的各项都是正数,所以
的各项都是正数,所以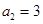 ,
,
(2)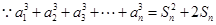 , ①
, ① , ②
, ②
由①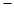 ②得
②得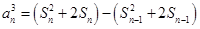 ,
,
化简得到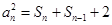 , ③
, ③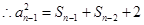 ,④
,④
由③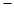 ④得
④得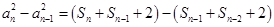 ,
,
化简得到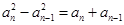 ,即
,即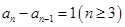 ,
,
当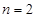 时,
时,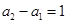 ,所以
,所以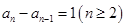 ,
,
所以数列 是一个以
是一个以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,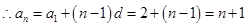 ;
;
(3)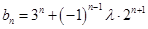 ,
,
因为对任意的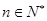 ,都有
,都有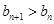 恒成立,即有
恒成立,即有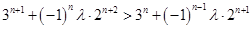 ,
,
化简得 ,
,
当 为奇数时,
为奇数时, 恒成立,
恒成立, ,即
,即 ,
,
当 为偶数时,
为偶数时,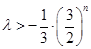 恒成立,
恒成立,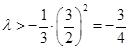 ,即
,即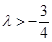 ,
,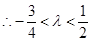 ,故实数
,故实数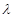 的取值范围是
的取值范围是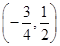 .
.
考点:1.定义法求数列的通项公式;2.数列不等式恒成立;3.分类讨论

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
己知等差数列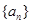 的首项为
的首项为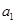 ,公差为
,公差为 ,其前
,其前 项和为
项和为 ,若直线
,若直线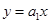 与圆
与圆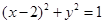 的两个交点关于直线
的两个交点关于直线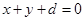 对称,则
对称,则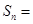 ( )
( )
A.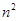 | B.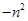 | C.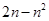 | D.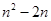 |
已知等差数列 的公差
的公差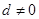 ,且
,且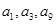 成等比数列,则
成等比数列,则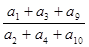 的值是( )
的值是( )
A.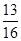 | B.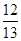 | C.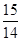 | D.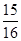 |
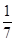 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是 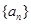 的前
的前 项和
项和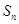 和通项
和通项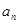 满足
满足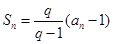 (
(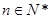 ,
,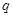 是大于0的常数,且
是大于0的常数,且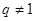 ),数列
),数列 是公比不为
是公比不为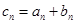 .
.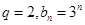 ,是否存在实数
,是否存在实数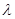 ,使数列
,使数列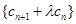 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数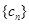 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的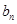 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.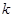 (
(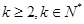 )的数列
)的数列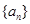 、
、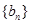 、
、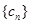 前
前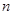 项的和分别为
项的和分别为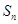 、
、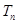 、
、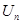 .已知集合
.已知集合 =
=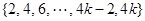 .
.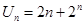 ,求数列
,求数列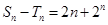
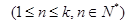 ,试研究
,试研究 和
和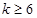 时是否存在符合条件的数列对(
时是否存在符合条件的数列对(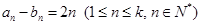 ,对于固定的
,对于固定的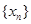 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为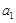 ,公差为
,公差为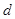 的无穷等差数列
的无穷等差数列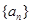 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项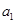 ,第三项
,第三项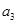 和第五项
和第五项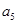 .
. 成等比数列,求
成等比数列,求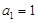 ,
, 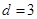 的无穷等差数列
的无穷等差数列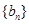 ,使得数列
,使得数列 ,公比为正整数
,公比为正整数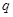 (
(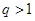 )的无穷等比数 列
)的无穷等比数 列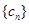 ,总可以找到一个子数列
,总可以找到一个子数列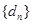 ,使得
,使得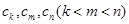 ,由
,由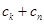 与
与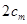 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?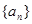 满足:
满足: 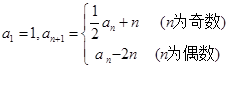
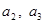 ;
; 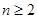 时,求
时,求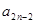 与
与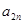 的关系式,并求数列
的关系式,并求数列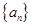 的前
的前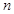 项和
项和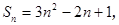 则它的通项公式是__________
则它的通项公式是__________