题目内容
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
【答案】(1)![]() ;(2)单调递增区间为
;(2)单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)根据题意分析可能曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,等价于
轴平行,等价于![]() ,从而
,从而![]() ;(2)由(1)可知
;(2)由(1)可知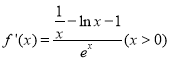 ,只需考虑分子
,只需考虑分子![]() 的正负性即可,而
的正负性即可,而![]() ,
,![]() 在
在![]() 上单调递减,再由
上单调递减,再由![]() ,故当
,故当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,∴单调递增区间为
单调递减,∴单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;(3)
;(3)![]() ,这是一指对相结合的函数,混在一起考虑其单调性比较复杂,因此考虑分开研究各自的取值情况:记
,这是一指对相结合的函数,混在一起考虑其单调性比较复杂,因此考虑分开研究各自的取值情况:记![]() ,
,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() .
.
② 记![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,综合①,②可知,
,综合①,②可知,![]() .
.
试题解析:(1)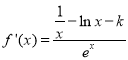 ,依题意,
,依题意,![]() 为所求;
为所求;
(2)由(1)可知,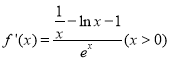 ,记
,记![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递减,又∵
上单调递减,又∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,∴单调递增区间为
单调递减,∴单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;
(3)![]() ,
,
① 记![]() ,
,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() .
.
② 记![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,综合①,②可知,
,综合①,②可知,![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目