题目内容
如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(Ⅰ)证明:BD⊥AA1;(Ⅱ)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
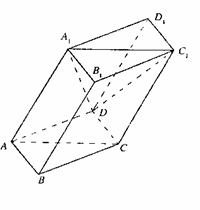
在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD

……………………6分
(Ⅱ)存在这样的点P,连接B1C,因为A1B1![]() AB
AB![]() DC
DC
∴四边形A1B1CD为平行四边形。∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP
因B1B![]() CC1,
CC1,
∴BB1![]() CP ∴四边形BB1CP为平行四边形
CP ∴四边形BB1CP为平行四边形
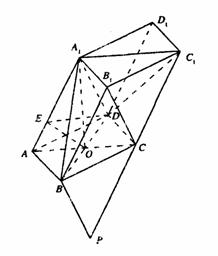 则BP//B1C ∴BP//A1D ∴BP//平面DA1C1
则BP//B1C ∴BP//A1D ∴BP//平面DA1C1

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
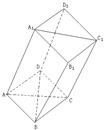 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.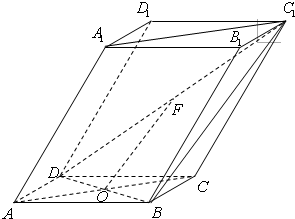 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.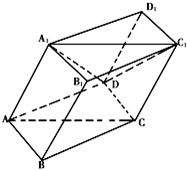 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?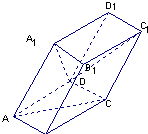 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°