题目内容
在等比数列{an}中,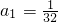 ,当n≥11时,an>1恒成立,则公比q的取值范围是:
,当n≥11时,an>1恒成立,则公比q的取值范围是:
- A.0<q<1
- B.q>1
- C.q>2
- D.q>

D
分析:根据题意结合等比数列的单调性可得,数列{an}是递增数列,故当n≥11时,an>1恒成立,即a11>1,利用等比数列的通项公式表示出a11,代入不等式求解即可.
解答:∵等比数列{an}中,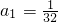 >0,当n≥11时,an>1恒成立,
>0,当n≥11时,an>1恒成立,
∴q>1,即数列{an}是各项均为正数的递增数列,
∴当n≥11时,an>1恒成立,即a11>1,
∵a11= •q10>1,
•q10>1,
∴q10>32,
∴q2>2,
∴q> ,
,
故选D.
点评:本题通过解不等式问题,综合考查了等比数列的单调性和通项公式,难度中等.
分析:根据题意结合等比数列的单调性可得,数列{an}是递增数列,故当n≥11时,an>1恒成立,即a11>1,利用等比数列的通项公式表示出a11,代入不等式求解即可.
解答:∵等比数列{an}中,
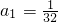 >0,当n≥11时,an>1恒成立,
>0,当n≥11时,an>1恒成立,∴q>1,即数列{an}是各项均为正数的递增数列,
∴当n≥11时,an>1恒成立,即a11>1,
∵a11=
 •q10>1,
•q10>1,∴q10>32,
∴q2>2,
∴q>
 ,
,故选D.
点评:本题通过解不等式问题,综合考查了等比数列的单调性和通项公式,难度中等.

练习册系列答案
相关题目
在等比数列{an}中,若a1=1,公比q=2,则a12+a22+…+an2=( )
| A、(2n-1)2 | ||
B、
| ||
| C、4n-1 | ||
D、
|