题目内容
已知函数f(x)=x+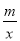 ,且f(1)=2.
,且f(1)=2.
(1)求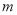 ;
;
(2)判断 的奇偶性;
的奇偶性;
(3)函数 在
在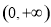 上是增函数还是减函数?并证明.
上是增函数还是减函数?并证明.
(1)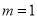 ;(2)奇函数;(3)增函数.
;(2)奇函数;(3)增函数.
【解析】
试题分析:(1)根据题意将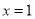 带入
带入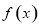 的解析式中,得到关于
的解析式中,得到关于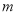 的方程,进而求得
的方程,进而求得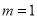 的值;(2)根据(1)得到
的值;(2)根据(1)得到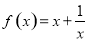 ,再根据函数奇偶性的定义判断其奇偶性,首先确定定义域关于原点对称,其次判断
,再根据函数奇偶性的定义判断其奇偶性,首先确定定义域关于原点对称,其次判断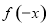 与
与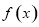 的关系,得到
的关系,得到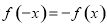 ,则原函数为奇函数;(3)根据函数单调性的定义,首先在
,则原函数为奇函数;(3)根据函数单调性的定义,首先在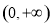 任取
任取 且
且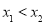 ,带入函数
,带入函数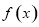 中,用作差法比较
中,用作差法比较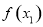 与
与 的大小,得到
的大小,得到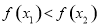 所以原函数在
所以原函数在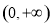 上为增函数.
上为增函数.
试题解析:(1)f(1)=1+m=2,m=1. 2分
(2)f(x)=x+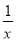 ,f(-x)=-x-
,f(-x)=-x-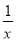 =-f(x),∴f(x)是奇函数. 6分
=-f(x),∴f(x)是奇函数. 6分
(3)设x1、x2是(1,+∞)上的任意两个实数,且x1<x2,则 7分
f(x1)-f(x2)=x1+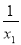 -(x2+
-(x2+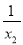 )=x1-x2+(
)=x1-x2+(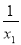 -
-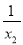 )
)
=x1-x2-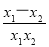 =(x1-x2)
=(x1-x2)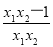 . 10分
. 10分
当1<x1<x2时,x1x2>1,x1x2-1>0,从而f(x1)-f(x2)<0,
即f(x1)<f(x2).
∴函数f(x)=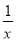 +x在(1,+∞)上为增函数. 12分
+x在(1,+∞)上为增函数. 12分
考点:1.函数解析式;2.函数奇偶性;3.函数单调性.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
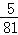 B.
B.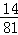 C.
C.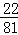 D.
D.
 ,圆
,圆 的面积为
的面积为 ,则
,则 .
. 为取整函数,
为取整函数, 是方程
是方程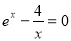 的根 (e为自然对数的底数),则
的根 (e为自然对数的底数),则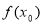 等于 ( )
等于 ( ) 的扇形的面积为( )
的扇形的面积为( ) B.
B.  C.
C.  D.
D.
 恒过定点
恒过定点 ,则
,则 _____________.
_____________.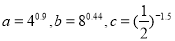 ,则 ( )
,则 ( ) ,则实数
,则实数 的值等于 .
的值等于 .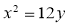 的焦点为
的焦点为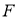 ,经过点
,经过点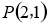 的直线
的直线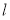 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为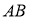 的中点,则
的中点,则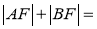 .
.