题目内容
14.当0<a<2时,直线l1:ax-2y=2a-4,直线${l_2}:2x+{a^2}y=2{a^2}+4$与坐标轴围成的一个四边形,求该四边形面积的最小值以及取得最小值时的a的值.分析 如图所示,联立$\left\{\begin{array}{l}{ax-2y=2a-4}\\{2x+{a}^{2}y=2{a}^{2}+4}\end{array}\right.$,解得yE=2.根据S四边形OCEA=S△BCE-S△OAB即可得出.
解答 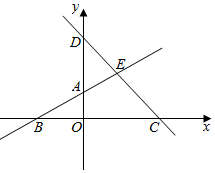 解:∵0<a<2,
解:∵0<a<2,
可得l1:ax-2y=2a-4,与坐标轴的交点A(0,-a+2),B(2-$\frac{4}{a}$,0).
l2:2x+a2y=2a2+4,与坐标轴的交点C(a2+2,0),D(0,2+$\frac{4}{{a}^{2}}$).
联立 $\left\{\begin{array}{l}{ax-2y=2a-4}\\{2x+{a}^{2}y=2{a}^{2}+4}\end{array}\right.$,
解得yE=2.
∴S四边形OCEA=S△BCE-S△OAB
=$\frac{1}{2}$|BC|•yE-$\frac{1}{2}$|OA|•|OB|
=a2+$\frac{4}{a}$-$\frac{1}{2}$×(2-a)×($\frac{4}{a}$-2)
=a2-a+4
=(a-$\frac{1}{2}$)2+$\frac{15}{4}$≥$\frac{15}{4}$,当a=$\frac{1}{2}$时取等号.
∴l1,l2与坐标轴围成的四边形面积的最小值为$\frac{15}{4}$.
点评 本题考查了相交直线、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在同一坐标系中,函数y=3-x与y=3x的图象之间的关系是( )
| A. | 关于原点对称 | B. | 关于直线y=x对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
6.直线2x+y+7=0的倾斜角为( )
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 不存在 |
4.已知直线l的斜率为$-\frac{{\sqrt{3}}}{3}$,则该直线l的倾斜角为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |