题目内容
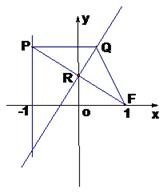
在平面直角坐标系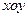 中,设点
中,设点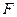 (1,0),直线
(1,0),直线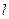 :
: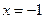 ,点
,点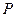 在直线
在直线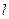 上移动,
上移动,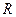 是线段
是线段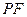 与
与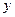 轴的交点,
轴的交点, 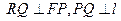 .
.
(Ⅰ)求动点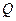 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记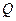 的轨迹的方程为
的轨迹的方程为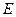 ,过点
,过点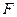 作两条互相垂直的曲线
作两条互相垂直的曲线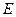 的弦
的弦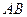 、
、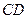 ,设
,设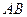 、
、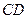 的中点分别为
的中点分别为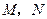 .求证:直线
.求证:直线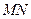 必过定点
必过定点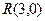 .
.
 中,设点
中,设点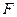 (1,0),直线
(1,0),直线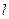 :
: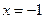 ,点
,点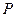 在直线
在直线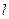 上移动,
上移动,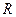 是线段
是线段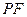 与
与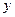 轴的交点,
轴的交点, 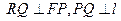 .
.(Ⅰ)求动点
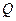 的轨迹的方程;
的轨迹的方程;(Ⅱ) 记
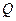 的轨迹的方程为
的轨迹的方程为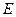 ,过点
,过点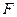 作两条互相垂直的曲线
作两条互相垂直的曲线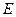 的弦
的弦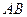 、
、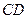 ,设
,设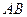 、
、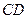 的中点分别为
的中点分别为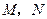 .求证:直线
.求证:直线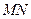 必过定点
必过定点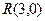 .
.
(Ⅰ)动点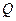 的轨迹
的轨迹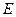 是以
是以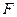 为焦点,
为焦点,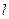 为准线的抛物线,其方程为:
为准线的抛物线,其方程为: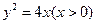 .
.
(Ⅱ)见解析
 的轨迹
的轨迹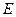 是以
是以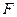 为焦点,
为焦点,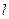 为准线的抛物线,其方程为:
为准线的抛物线,其方程为: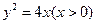 .
. (Ⅱ)见解析
(Ⅰ)依题意知,直线
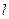 的方程为:
的方程为: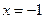 .点
.点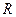 是线段
是线段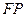 的中点,且
的中点,且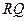 ⊥
⊥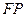 ,∴
,∴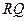 是线段
是线段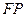 的垂直平分线.…………………….2分
的垂直平分线.…………………….2分∴
 是点
是点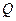 到直线
到直线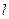 的距离.
的距离.∵点
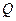 在线段
在线段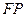 的垂直平分线,∴
的垂直平分线,∴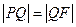 .…………4分
.…………4分故动点
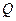 的轨迹
的轨迹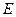 是以
是以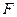 为焦点,
为焦点,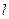 为准线的抛物线,其方程为:
为准线的抛物线,其方程为: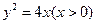 . ……….7分
. ……….7分(Ⅱ) 设
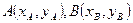 ,
,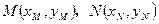 ,直线AB的方程为
,直线AB的方程为 …………….8分
…………….8分则
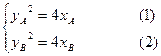
(1)—(2)得
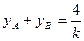 ,即
,即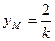 ,……………………………………9分
,……………………………………9分代入方程
 ,解得
,解得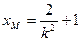 .
.所以点M的坐标为
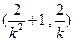 .……………………………………10分
.……………………………………10分同理可得:
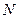 的坐标为
的坐标为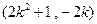 .
.直线
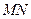 的斜率为
的斜率为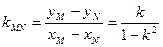 ,方程为
,方程为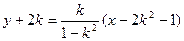 ,整理得
,整理得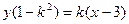 ,………………12分
,………………12分显然,不论
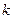 为何值,
为何值,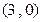 均满足方程,
均满足方程,所以直线
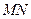 恒过定点
恒过定点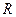
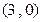 .………………14
.………………14
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
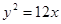 上的点
上的点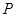 与焦点的距离为
与焦点的距离为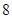 ,则
,则


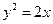 的焦点为F,过点M
的焦点为F,过点M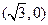 的直线与抛物线相交于两点,与抛物线的准线相交于点C,
的直线与抛物线相交于两点,与抛物线的准线相交于点C,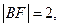 则
则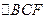 与
与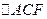 的面积之比
的面积之比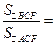 ______________.
______________.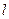 应设计为多少?
应设计为多少?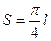 h)?
h)?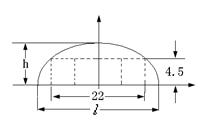
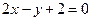 上的抛物线的标准方程为( )
上的抛物线的标准方程为( )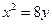
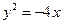
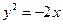 或
或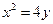
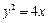 的焦点为F,
的焦点为F,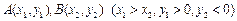 在抛物线上,且存在实数λ,使
在抛物线上,且存在实数λ,使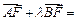 0,
0,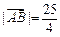 .
.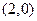 的距离和它到定直线
的距离和它到定直线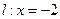 的距离相等,则点P的轨迹方程为_________.
的距离相等,则点P的轨迹方程为_________.