题目内容
若关于 的方程
的方程 =0在
=0在 上有解,则
上有解,则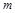 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
D
解析试题分析:∵x2-x-a-1=0在x∈[-1,1]上有解,∴a=x2-x-1,然后求解导数,a′=2x-1,,∴当x∈[-1, ]时函数x2-x-1单调递减,当x∈[
]时函数x2-x-1单调递减,当x∈[ ,1]时函数x2-x-1单调递增,∵当x=-1时,a=1;当x=
,1]时函数x2-x-1单调递增,∵当x=-1时,a=1;当x= 时,a=-
时,a=- ;
;
故实数a的范围为[- ,1].故答案为:[-
,1].故答案为:[- ,1],选D.
,1],选D.
考点:本题主要考查考查方程的根与函数之间的关系.考查根据导函数的正负判断函数的单调性,再由单调性求函数的值域的问题.
点评:解决该试题的关键是先将方程转化为a关于x的二次函数,然后对此函数进行求导运算判断函数在[-1,1]上的单调性,进而求出值域,即为a的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若奇函数 在
在 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在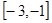 上( )
上( )
| A.是减函数,有最小值0 | B.是增函数,有最小值0 |
| C.是减函数,有最大值0 | D.是增函数,有最大值0 |
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
设函数 定义在实数集R上,
定义在实数集R上, ,且当
,且当 时
时 =
= ,则有 ( )
,则有 ( )
A. | B. |
C. | D. |
函数 的图象向左平移
的图象向左平移 个单位,所得的图形对应的函数是( )
个单位,所得的图形对应的函数是( )
A.偶函数,值域为 | B.奇函数,值域为 |
C.偶函数,值域为  | D.奇函数,值域为 |
已知函数 为奇函数,则
为奇函数,则 的值为( )
的值为( )
A. | B. | C. | D. |
方程 的实数解落在的区间是
的实数解落在的区间是
A. | B. | C. | D. |
设偶函数 的定义域为R,当
的定义域为R,当
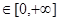 时,
时, 是增函数,则
是增函数,则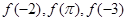 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
 与
与 的图象如所示,则函数
的图象如所示,则函数 的图象可能为( )
的图象可能为( )
