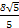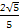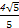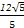题目内容
在△ABC中,A,B,C为三个内角,a,b,c为三条边,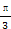 <C<
<C<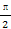 且
且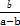 =
=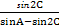 .
.
(1)判断△ABC的形状.
(2)若|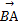 +
+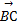 |=2,求
|=2,求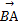 ·
·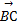 的取值范围.
的取值范围.
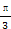 <C<
<C<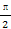 且
且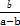 =
=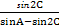 .
.(1)判断△ABC的形状.
(2)若|
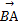 +
+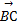 |=2,求
|=2,求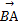 ·
·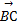 的取值范围.
的取值范围.(1) △ABC为等腰三角形 (2) ( ,1)
,1)
 ,1)
,1)(1)由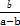 =
=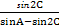 及正弦定理有:
及正弦定理有:
sinB="sin" 2C,
∴B=2C或B+2C=π.
若B=2C,且 <C<
<C< ,
,
∴ π<B<π,B+C>π(舍).
π<B<π,B+C>π(舍).
∴B+2C=π,则A=C,
∴△ABC为等腰三角形.
(2)∵|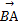 +
+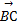 |=2,
|=2,
∴a2+c2+2ac·cosB=4,
∵a=c,∴cosB= ,
,
而cosB="-cos" 2C,
∴ <cosB<1,
<cosB<1,
∴1<a2< ,
,
∴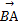 ·
·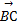 =2-a2,
=2-a2,
故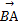 ·
·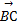 ∈(
∈( ,1).
,1).
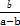 =
=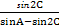 及正弦定理有:
及正弦定理有:sinB="sin" 2C,
∴B=2C或B+2C=π.
若B=2C,且
 <C<
<C< ,
,∴
 π<B<π,B+C>π(舍).
π<B<π,B+C>π(舍).∴B+2C=π,则A=C,
∴△ABC为等腰三角形.
(2)∵|
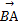 +
+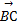 |=2,
|=2,∴a2+c2+2ac·cosB=4,
∵a=c,∴cosB=
 ,
,而cosB="-cos" 2C,
∴
 <cosB<1,
<cosB<1,∴1<a2<
 ,
,∴
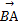 ·
·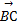 =2-a2,
=2-a2,故
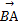 ·
·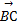 ∈(
∈( ,1).
,1).
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
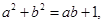 以AB为边向△ABC外作等边三角形△ABD.
以AB为边向△ABC外作等边三角形△ABD.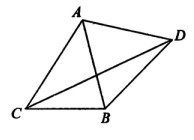
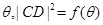 .试求函数
.试求函数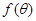 的最大值及
的最大值及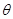 的值.
的值.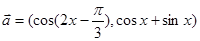 ,
,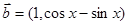 ,函数
,函数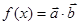 .
.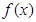 的单调递增区间;
的单调递增区间;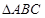 中,内角
中,内角 的对边分别为
的对边分别为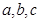 ,已知
,已知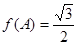 ,
,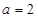 ,
,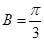 ,求
,求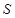 .
. 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,
,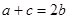 ;
; ,求
,求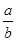 的值.
的值.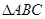 中,角
中,角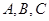 的对边分别为
的对边分别为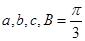 ,
,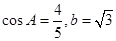 。
。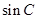 的值;
的值;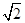 (B)2
(B)2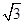 (C)
(C)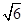 -
-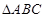 中,已知
中,已知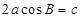 ,
,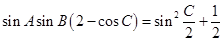 ,则
,则
 ,A=
,A=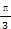 ,cosB=
,cosB=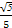 ,则b=( )
,则b=( )