题目内容
已知集合A={x|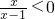
}，b={x|x
＜1}，A∩B=
- A.[0，1]
- B.（0，1）
- C.[0，1）
- D.?
B
分析：利用解分式不等式和根式不等式，分别求出集合A、B，然后在求A∩B即可．
解答：由，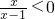
∴0＜x＜1
∴A=（0，1）
又x＜1，
∴0≤x＜1，
∴B=[0，1）．
∴A∩B=（0，1）
故选B．
点评：本题考查集合运算，同时考查解分式不等式和根式不等式．要注意集合的元素．属简单题
分析：利用解分式不等式和根式不等式，分别求出集合A、B，然后在求A∩B即可．
解答：由
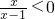，∴0＜x＜1
∴A=（0，1）
又x
＜1，∴0≤x＜1，
∴B=[0，1）．
∴A∩B=（0，1）
故选B．
点评：本题考查集合运算，同时考查解分式不等式和根式不等式．要注意集合的元素．属简单题
练习册系列答案
相关题目