题目内容
定义:若存在常数k,使得对定义域D内的任意两个不同的实数x1,x2,均有|f(x1)﹣f(x2)|≤k(x1﹣x2)成立,则称函数f(x)在定义域D上满足利普希茨条件.对于函数f(x)=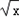 (x≥1)满足利普希茨条件,则常数k的最小值应是
(x≥1)满足利普希茨条件,则常数k的最小值应是
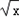 (x≥1)满足利普希茨条件,则常数k的最小值应是
(x≥1)满足利普希茨条件,则常数k的最小值应是 [ ]
A.2
B.1
C.
D.
B.1
C.

D.

C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目