题目内容
记Sn为数列{an}的前n项和,给出两个数列:
(Ⅰ)5,3,1,-1,-3,-5,-7,…
(Ⅱ)-14,-10,-6,-2,2,6,10,14,18,…
(1)对于数列(Ⅰ),计算S1,S2,S4,S5;
对于数列(Ⅱ),计算S1,S3,S5,S7;
(2)根据上述结果,对于存在正整数k,满足ak+ak+1=0的这一类等差数列{an}的和的规律,猜想一个正确的结论,并加以说明.
解 (1)对于数列(Ⅰ),S1=S5=5,S2=S4=8;
对于数列(Ⅱ),S1=S7=-14,S3=S5=-30.
(2)对于等差数列{an},当ak+ak+1=0时,
猜想Sn=S2k-n(n≤2k,n,k∈N*).
下面给出证明:
设等差数列{an}的前项为a1,公差为d.
∵ak+ak+1=0,∴a1+(k-1)d+a1+kd=0,
∴2a1=(1-2k)d.
 ∴S2k-n=Sn,猜想正
∴S2k-n=Sn,猜想正 确.
确.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 、
、 、
、 、
、 、
、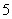 、
、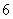 个点)两次,落在水平桌面后,记正面朝上的点数分别为
个点)两次,落在水平桌面后,记正面朝上的点数分别为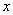 ,
,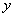 ,设事件
,设事件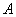 为“
为“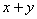 为偶数”, 事件
为偶数”, 事件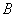 为
为 ”,则概率
”,则概率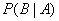 等于 。
等于 。 a+
a+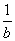 ,b+
,b+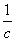 ,c+
,c+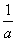 的说法正确的是________.
的说法正确的是________.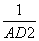 =
=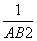 +
+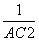 成立.那么在四面体A-BCD中,
成立.那么在四面体A-BCD中, 类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由.
类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由. (其中x∈R且x≠
(其中x∈R且x≠ ),求证:经过这个
),求证:经过这个 函数图象上任意两个不同点的直线不平行于x轴.
函数图象上任意两个不同点的直线不平行于x轴.