题目内容
如图,已知正三棱柱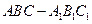 的各棱长都为
的各棱长都为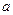 ,
,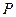 为棱
为棱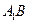 上的动点.
上的动点.

(Ⅰ)当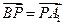 时,求证:
时,求证: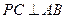 ;
;
(Ⅱ)若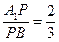 ,求二面角
,求二面角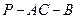 的大小;
的大小;
(Ⅲ)在(Ⅱ)的条件下,求点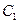 到平面
到平面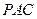 的距离.
的距离.
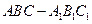 的各棱长都为
的各棱长都为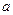 ,
,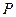 为棱
为棱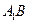 上的动点.
上的动点.
(Ⅰ)当
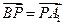 时,求证:
时,求证: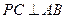 ;
; (Ⅱ)若
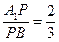 ,求二面角
,求二面角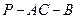 的大小;
的大小; (Ⅲ)在(Ⅱ)的条件下,求点
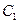 到平面
到平面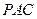 的距离.
的距离. ,
,
解:(Ⅰ)当
 时,取
时,取 的中点
的中点 ,连接
,连接 ,因为
,因为 为正三角形,
为正三角形,
|



|
|
 ,由于
,由于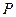 为
为 的中点时,
的中点时, ∵
∵ 平面
平面 ,∴
,∴ 平面
平面 ,∴
,∴ .
. 
|
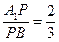 时,过
时,过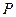 作
作 于
于 ,如图所示,
,如图所示,
|



 则
则 底面
底面 ,过
,过 作
作 于
于 ,连结
,连结 ,
, 则
则 ,
,


|
|
 为二面角
为二面角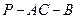 的平面角,
的平面角, 又
又 ,
,

又

 ,
,
 ,
,即二面角
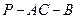 的大小为
的大小为 .
. (Ⅲ) 设
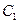 到面
到面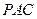 的距离为
的距离为 ,则
,则
 ,
, 平面
平面 ,
, 即为
即为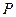 点到平面
点到平面 的距离,
的距离,又
 ,
, 即
即
解得
 ,即
,即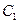 到平面
到平面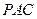 的距离为
的距离为 .
. 
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目






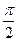 ,AD=
,AD=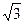 ,EF=2.
,EF=2.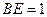 ,且二面角A—EF—C的大小为
,且二面角A—EF—C的大小为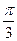 ,求
,求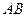 的长。
的长。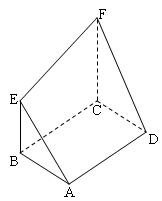
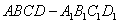 中,
中,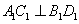 ,
,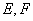 分别是
分别是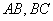 的中点.
的中点.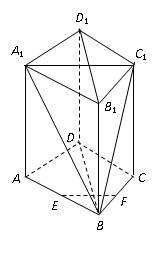
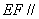 平面
平面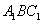 ;
;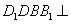 平面
平面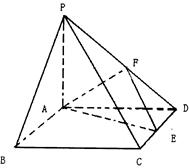
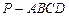 的底面为正方形,
的底面为正方形,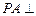 平面
平面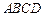 ,且
,且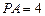 ,
,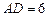 ,
,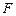 ,
,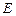 分别是线段
分别是线段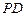 ,
,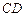 的中点.
的中点.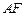 和
和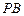 所成角的余弦值;
所成角的余弦值;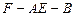 平面角的余弦值.
平面角的余弦值.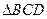 与
与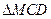 都是边长为2的正三角形,
都是边长为2的正三角形,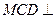 平面
平面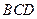 ,
,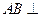 平面
平面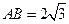 .
.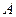 到平面
到平面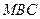 的距离;
的距离;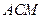 与平面
与平面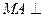 平面ABCD,MA//PB,PB=AB=2MA=2。
平面ABCD,MA//PB,PB=AB=2MA=2。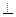 面PAC;
面PAC;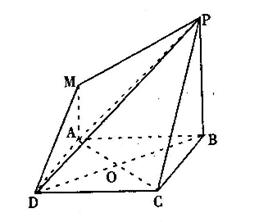 (3)求直线BD和平面PMD所成角的正弦值。
(3)求直线BD和平面PMD所成角的正弦值。 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。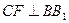 ;
;
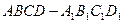 的棱长是2,
的棱长是2,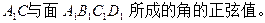
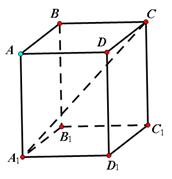
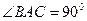 ,
,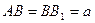 ,直线B1C与平面ABC成30°角。
,直线B1C与平面ABC成30°角。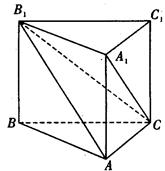
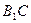 —A的正切值。
—A的正切值。