题目内容
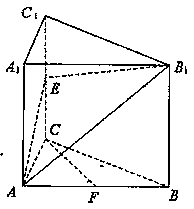
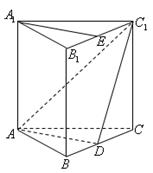
如图,已知直三棱柱ABC—A1B1C1,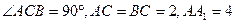 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。
(1)求证: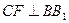 ;
;
(2)求四棱锥A—ECBB1的体积;
(3)判断直线CF和平面AEB1的位置关系,并加以证明。
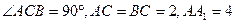 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。(1)求证:
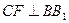 ;
;(2)求四棱锥A—ECBB1的体积;
(3)判断直线CF和平面AEB1的位置关系,并加以证明。

4, 平面AEB1
平面AEB1
 平面AEB1
平面AEB1解: (1)证明: 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,
 平面ABC 1分
平面ABC 1分
又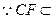 平面ABC, 2分
平面ABC, 2分
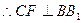 3分
3分
(2)解: 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,
 平面ABC,
平面ABC,
又 平面ABC
平面ABC


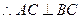
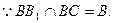
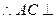 平面ECBB1 6分
平面ECBB1 6分
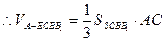 7分
7分
 是棱CC1的中点,
是棱CC1的中点,
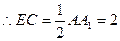

 8分
8分
 (3)解:CF//平面AEB1,证明如下:
(3)解:CF//平面AEB1,证明如下:
取AB1的中点G,联结EG,FG
 分别是棱AB、AB1中点
分别是棱AB、AB1中点

又
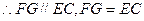
 四边形FGEC是平行四边形
四边形FGEC是平行四边形 
又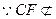 平面AEB,
平面AEB, 平面AEB1,
平面AEB1,
 平面AEB1。12分
平面AEB1。12分
 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱, 平面ABC 1分
平面ABC 1分又
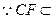 平面ABC, 2分
平面ABC, 2分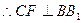 3分
3分(2)解:
 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱, 平面ABC,
平面ABC,又
 平面ABC
平面ABC

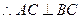
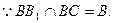
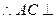 平面ECBB1 6分
平面ECBB1 6分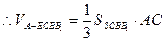 7分
7分 是棱CC1的中点,
是棱CC1的中点,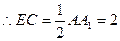

 8分
8分 (3)解:CF//平面AEB1,证明如下:
(3)解:CF//平面AEB1,证明如下:取AB1的中点G,联结EG,FG
 分别是棱AB、AB1中点
分别是棱AB、AB1中点
又

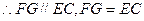
 四边形FGEC是平行四边形
四边形FGEC是平行四边形 
又
 平面AEB,
平面AEB, 平面AEB1,
平面AEB1, 平面AEB1。12分
平面AEB1。12分
练习册系列答案
相关题目
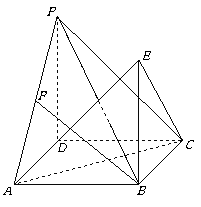
 中,
中,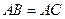 ,点
,点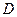 在边
在边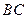 上,
上,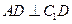 。
。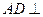 平面
平面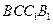 ;
;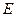 是
是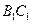 的中点,求证:
的中点,求证: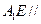 平面
平面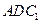 .
.
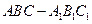 的各棱长都为
的各棱长都为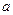 ,
,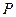 为棱
为棱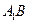 上的动点.
上的动点.
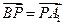 时,求证:
时,求证: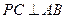 ;
; 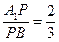 ,求二面角
,求二面角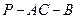 的大小;
的大小; 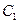 到平面
到平面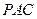 的距离.
的距离.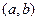 为圆心,以
为圆心,以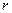 为半径的圆的方程为
为半径的圆的方程为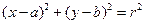 ,类似的在空间以点
,类似的在空间以点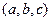 为球心,以
为球心,以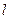 ,
,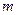 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是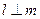 ,
,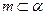 ,则
,则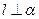
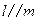 ,则
,则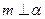
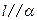 ,
,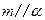 ,则
,则
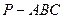 中,
中,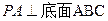 ,
,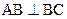 ,
,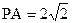 ,
,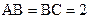 ,若
,若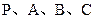 四点在同一个球面上,则在球面上
四点在同一个球面上,则在球面上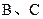 两点之间的球面距离是_____ .
两点之间的球面距离是_____ .