题目内容
已知
=（-5，6），
=（-3，2），
=（x，y），若
-3
+2
=
，则
等于（ ）A．
=（-2，6）B．
=（-4，0）C．
=（7，6）D．
=（-2，0）
【答案】分析：将平面向量的坐标代入等式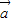
-3
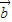+2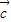
=
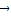，然后根据相等向量的坐标关系建立等式关系，解之即可求出所求．
解答：解：∵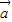
-3
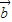+2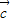
=
，
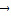∴（-5，6）-3（-3，2）+2（x，y）=（0，0）
即（4+2x，2y）=（0，0）
∴
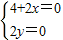解得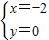
∴
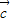=（-2，0）
故选D．
点评：本题主要考查了平面向量坐标表示的应用，以及平面向量的坐标运算，同时考查了相等向量的坐标关系，属于基础题．
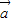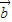-3+2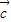=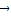，然后根据相等向量的坐标关系建立等式关系，解之即可求出所求．解答：解：∵
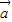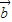-3+2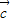=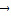，∴（-5，6）-3（-3，2）+2（x，y）=（0，0）
即（4+2x，2y）=（0，0）
∴
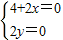解得∴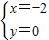
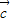=（-2，0）故选D．
点评：本题主要考查了平面向量坐标表示的应用，以及平面向量的坐标运算，同时考查了相等向量的坐标关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=(-5，6)，
=(6，5)，则
与
（ ）
| a |
| b |
| a |
| b |
| A、垂直 | B、不垂直也不平行 |
| C、平行且同向 | D、平行且反向 |
B.
C.
D.