题目内容
如果函数y=3sin(2x+φ)的图象关于点(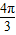 ,0)成中心对称,那么|φ|的最小值为( )
,0)成中心对称,那么|φ|的最小值为( )A.
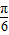
B.
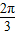
C.
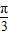
D.
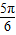
【答案】分析:根据函数y=3sin(2x+φ)的图象关于点(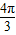 ,0)中心对称,令x=
,0)中心对称,令x=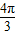 代入函数使其等于0,求出φ的值,从而求得|φ|的最小值.
代入函数使其等于0,求出φ的值,从而求得|φ|的最小值.
解答:解:根据函数y=3sin(2x+φ)的图象关于点(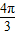 ,0)中心对称,可得3sin(2×
,0)中心对称,可得3sin(2×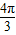 +φ)=0,
+φ)=0,
故有 2×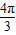 +φ=kπ,k∈z,由此可得∅=kπ-
+φ=kπ,k∈z,由此可得∅=kπ-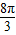 ,k∈z,
,k∈z,
令k=3,可得|φ|的最小值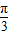 ,
,
故选C.
点评:本题主要考查复合余弦函数的对称性的应用,属基础题.
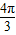 ,0)中心对称,令x=
,0)中心对称,令x=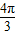 代入函数使其等于0,求出φ的值,从而求得|φ|的最小值.
代入函数使其等于0,求出φ的值,从而求得|φ|的最小值.解答:解:根据函数y=3sin(2x+φ)的图象关于点(
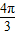 ,0)中心对称,可得3sin(2×
,0)中心对称,可得3sin(2×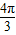 +φ)=0,
+φ)=0,故有 2×
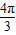 +φ=kπ,k∈z,由此可得∅=kπ-
+φ=kπ,k∈z,由此可得∅=kπ-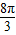 ,k∈z,
,k∈z,令k=3,可得|φ|的最小值
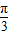 ,
,故选C.
点评:本题主要考查复合余弦函数的对称性的应用,属基础题.

练习册系列答案
相关题目
 ,0)中心对称,则ϕ= .
,0)中心对称,则ϕ= . ,0)中心对称,则ϕ= .
,0)中心对称,则ϕ= .