题目内容
若实数x的取值满足条件 ,求函数
,求函数 的最大值与最小值.
的最大值与最小值.
解:
令 ,对称轴为
,对称轴为
则当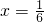 时,
时, ;当
;当 时,Umax=1
时,Umax=1
所以 ,又y=log2U在
,又y=log2U在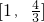 上递增
上递增
所以当U=1即 时,ymin=0
时,ymin=0
当 即
即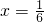 时,
时,
分析:由已知中件 ,我们易求出实数x的取值范围,令
,我们易求出实数x的取值范围,令 ,则我们可以求出U的取值范围,然后根据对数函数的单调性,即可求出满足条件的函数
,则我们可以求出U的取值范围,然后根据对数函数的单调性,即可求出满足条件的函数 的最大值与最小值.
的最大值与最小值.
点评:本题考查的知识点是对数函数的值域与最值,其中利用指数函数的单调性根据已知求出满足条件的x的取值范围,是解答本题的关键.

令
 ,对称轴为
,对称轴为
则当
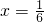 时,
时, ;当
;当 时,Umax=1
时,Umax=1所以
 ,又y=log2U在
,又y=log2U在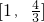 上递增
上递增所以当U=1即
 时,ymin=0
时,ymin=0当
 即
即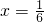 时,
时,
分析:由已知中件
 ,我们易求出实数x的取值范围,令
,我们易求出实数x的取值范围,令 ,则我们可以求出U的取值范围,然后根据对数函数的单调性,即可求出满足条件的函数
,则我们可以求出U的取值范围,然后根据对数函数的单调性,即可求出满足条件的函数 的最大值与最小值.
的最大值与最小值.点评:本题考查的知识点是对数函数的值域与最值,其中利用指数函数的单调性根据已知求出满足条件的x的取值范围,是解答本题的关键.

练习册系列答案
相关题目
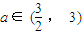 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点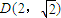 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;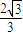 ,求实数x的取值范围.
,求实数x的取值范围.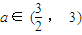 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点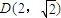 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;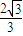 ,求实数x的取值范围.
,求实数x的取值范围.