题目内容
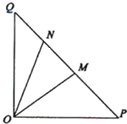 (2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
(2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2| 2 |
(Ⅰ)若OM=
| 5 |
(Ⅱ)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
分析:(Ⅰ)在△OMP中,利用∠OPM=45°,OM=
,OP=2
,通过余弦定理,求PM的长;
(Ⅱ)利用正弦定理求出ON、OM,表示出△OMN的面积,利用两角和与差的三角函数化简函数我一个角的一个三角函数的形式,通过角α的范围,得到相位的范围,然后利用正弦函数的值域求解三角形面积的最小值,求出面积的最小值.
| 5 |
| 2 |
(Ⅱ)利用正弦定理求出ON、OM,表示出△OMN的面积,利用两角和与差的三角函数化简函数我一个角的一个三角函数的形式,通过角α的范围,得到相位的范围,然后利用正弦函数的值域求解三角形面积的最小值,求出面积的最小值.
解答:解:(Ⅰ)在△OMP中,∠OPM=45°,OM=
,OP=2
,
由余弦定理可得,OM2=OP2+MP2-2×OP•MPcos45°,
解得PM的长为1或3;
(Ⅱ)设∠POM=α,0°≤α≤60°,在△OMP中,由正弦定理可得:
=
,
OM=
,
同理,ON=
,
故S△OMN=
OM•ONsin∠MON
=
×
=
=
=
=
=
因为0°≤α≤60°,所以30°≤2α+30°≤150°,
所以当α=30°时,sin(2α+30°)的最大值为1,
此时,△OMN的面积最小,面积的最小值8-4
.
| 5 |
| 2 |
由余弦定理可得,OM2=OP2+MP2-2×OP•MPcos45°,
解得PM的长为1或3;
(Ⅱ)设∠POM=α,0°≤α≤60°,在△OMP中,由正弦定理可得:
| OM |
| sin∠OPM |
| OP |
| sin∠OMP |
OM=
| OPsin45° |
| sin(45°+α) |
同理,ON=
| OPsin45° |
| sin(75°+α) |
故S△OMN=
| 1 |
| 2 |
=
| 1 |
| 4 |
| OP2sin245° |
| sin(45°+α)sin(75°+α) |
=
| 1 |
| sin(45°+α)sin(45°+α+30°) |
=
| 1 | ||||||
sin(45°+α)[
|
=
| 1 | ||||||
|
=
| 1 | ||||||||||
|
=
| 1 | ||||||
|
因为0°≤α≤60°,所以30°≤2α+30°≤150°,
所以当α=30°时,sin(2α+30°)的最大值为1,
此时,△OMN的面积最小,面积的最小值8-4
| 3 |
点评:本题考查正弦定理与余弦定理在三角形中的应用,两角和与差的三角函数的应用,三角形的最值的求法,考查计算能力与转化思想的应用.

练习册系列答案
相关题目
 (2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC,
(2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC,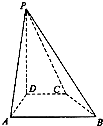 (2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.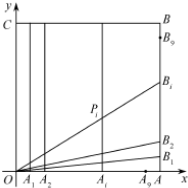 (2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点
(2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)