题目内容
(本题满分12分)如图,三角形 和梯形
和梯形 所在的平面互相垂直,
所在的平面互相垂直,  ,
, ,
, 是线段
是线段 上一点,
上一点, .
.

(Ⅰ)当 时,求证:
时,求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)是否存在点 满足
满足 平面
平面 ?并说明理由.
?并说明理由.
(Ⅰ)见解析;(Ⅱ) ;(Ⅲ)不存在点G,理由见解析
;(Ⅲ)不存在点G,理由见解析
【解析】
试题分析:(Ⅰ)取AB中点D,连接GD,CD, 1分
又GB=GF,所以 .
.
因为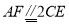 ,所以
,所以 ,
,
四边形GDCE是平行四边形, 2分
所以
因为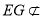 平面ABC,CD
平面ABC,CD 平面ABC
平面ABC
所以EG∥平面ABC. 4分

(Ⅱ)因为平面ABC⊥平面ACEF,平面ABC∩平面ACEF=AC,
且AF⊥AC,所以AF⊥平面ABC,所以AF⊥AB,AF⊥BC 5分
因为BC⊥AB,所以BC⊥平面ABF.如图,以A为原点,建立空间直角坐标系A-xyz.
则F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1), 6分
 是平面ABF的一个法向量.
是平面ABF的一个法向量.
设平面BEF的法向量 ,则
,则
 ,即
,即
令y=1,则z=-2,x=-2,所以 ,
,
所以 , 8分
, 8分
故二面角E-BF-A的正弦值为 。 9分.
。 9分.

(Ⅲ)因为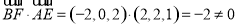 ,所以BF与AE不垂直, 11分
,所以BF与AE不垂直, 11分
所以不存在点G满足BF⊥平面AEG. 12分
考点:本题考查线面平行的判定,线面垂直的判定,二面角的求法,利用空间向量解决面面角,直线与平面的
位置关系

练习册系列答案
相关题目
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 轴上的椭圆
轴上的椭圆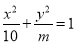 的长轴长为8,则
的长轴长为8,则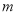 等于 ( )
等于 ( )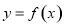 对于任意的
对于任意的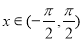 满足
满足 (其中
(其中 是函数
是函数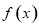 的导函数),则下列不等式不成立的是( )
的导函数),则下列不等式不成立的是( )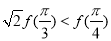 B.
B.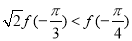
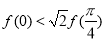 D.
D.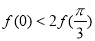
 ,命题
,命题 ,则
,则 是真命题,
是真命题,
 :
: 

 中,若
中,若 ,则角B= 。
,则角B= 。 ,
, ,曲线
,曲线 及
及 轴所围成的封闭图形的面积是 ( )
轴所围成的封闭图形的面积是 ( ) B.
B. C.
C. D.
D.
 的共轭复数为_______.
的共轭复数为_______. .
. ,求a,b;
,求a,b; ,求b.
,求b.