题目内容
比较下列每组数的大小(写出解答过程,将结果从小到大排列并用小于号连接起来):
(1)a=log
,b=log
,c=log
+log
;
(2)a=(
)-1,b=2
×2-log
÷
,c=7;
(3)a=
,b=
,c=
.
(1)a=log
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
(2)a=(
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
(3)a=
| 2 |
| 3 | 3 |
| 5 | 5 |
分析:(1)使用对数的运算法则和对数的换底公式分别化简,即可比较其大小;
(2)使用指数的运算法则先化简,进而可比较其大小;
(3)把其根指数化为相同,再利用幂函数的单调性即可比较其大小.
(2)使用指数的运算法则先化简,进而可比较其大小;
(3)把其根指数化为相同,再利用幂函数的单调性即可比较其大小.
解答:解:(1)∵a=log
=log
(
)2=2,b=log
=log
(
)3=3,
c=log
(
×
)=log
=
=
=log310,∵9<10<27,∴2<log310<3,
∴a<c<b.
(2)∵a=(
)-1=(6-1)-1=6;由log
=log
(
)2=2,∴b=2
-log
-
=21-2=
;c=7.
∴b<a<c.
(3)∵a=
=
,b=
=
,而
<
,∴a<b.
∵a=
=
,c=
=
,而
<
,∴c<a.
∴c<a<b.
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
c=log
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 10 |
lg
| ||
lg
|
| -lg10 |
| -lg3 |
∴a<c<b.
(2)∵a=(
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴b<a<c.
(3)∵a=
| 6 | 23 |
| 6 | 8 |
| 6 | 32 |
| 6 | 9 |
| 6 | 8 |
| 6 | 9 |
∵a=
| 10 | 25 |
| 10 | 32 |
| 10 | 52 |
| 10 | 25 |
| 10 | 25 |
| 10 | 32 |
∴c<a<b.
点评:掌握指数函数、对数函数及幂函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,b=
,b= ,c=
,c= +
+ ;
; )-1,b=
)-1,b=
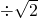 ,c=7;
,c=7; ,b=
,b=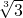 ,c=
,c= .
. ,b=
,b= ,c=
,c= +
+ ;
; )-1,b=
)-1,b=
 ,c=7;
,c=7; ,b=
,b= ,c=
,c= .
. ,b=
,b= ,c=
,c= +
+ ;
; )-1,b=
)-1,b=
 ,c=7;
,c=7; ,b=
,b= ,c=
,c= .
.