题目内容
已知a= sinxdx,则函数f (x)=x3-(a+1)x的极小值等于________.
sinxdx,则函数f (x)=x3-(a+1)x的极小值等于________.
-2
分析:利用微积分基本定理和导数研究函数的单调性极值即可得出.
解答:∵ =
= =2.
=2.
∴f(x)=x3-3x,∴f′(x)=3x2-3=3(x+1)(x-1),
令f′(x)=0,x=±1.列表如下:
由表格可知:当x=1时,函数f(x)取得极小值,f(1)=1-3=-2.
故答案为-2.
点评:熟练掌握微积分基本定理及利用导数研究函数的单调性极值是解题的关键.
分析:利用微积分基本定理和导数研究函数的单调性极值即可得出.
解答:∵
 =
= =2.
=2.
∴f(x)=x3-3x,∴f′(x)=3x2-3=3(x+1)(x-1),
令f′(x)=0,x=±1.列表如下:
由表格可知:当x=1时,函数f(x)取得极小值,f(1)=1-3=-2.
故答案为-2.
点评:熟练掌握微积分基本定理及利用导数研究函数的单调性极值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 sinxdx则f[f(
sinxdx则f[f( )]=1+cos1
)]=1+cos1 sinxdx,则f[f(
sinxdx,则f[f(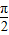 )]=( )
)]=( ) sinxdx,则函数f (x)=x3-(a+1)x的极小值等于 .
sinxdx,则函数f (x)=x3-(a+1)x的极小值等于 . sinxdx则f[f(
sinxdx则f[f( )]=1+cos1
)]=1+cos1