题目内容
为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用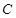 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度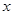 (单位:
(单位: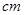 )满足关系:
)满足关系: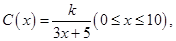
若不建隔热层,每年能源消耗费用为8万元。设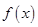 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求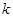 的值及
的值及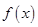 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用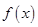 最小,并求最小值.
最小,并求最小值.
【答案】
(Ⅰ)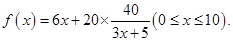 ;(Ⅱ)当
;(Ⅱ)当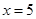 时,最小值为70.
时,最小值为70.
【解析】
试题分析:(Ⅰ)由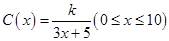 ,及若不建隔热层,每年能源消耗费用为8万元,即
,及若不建隔热层,每年能源消耗费用为8万元,即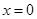 时,
时,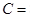
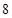 ,设
,设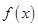 为隔热层建造费用与20年的能源消耗费用之和,每厘米厚的隔热层建造成本为6万元,厚度
为隔热层建造费用与20年的能源消耗费用之和,每厘米厚的隔热层建造成本为6万元,厚度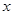 厘米的隔热层建造成本为
厘米的隔热层建造成本为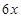 万元,建筑物每年的能源消耗费用
万元,建筑物每年的能源消耗费用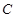 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度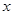 (单位:
(单位: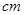 )满足关系:
)满足关系: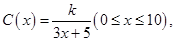 20年的能源消耗费用为
20年的能源消耗费用为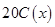 ,故
,故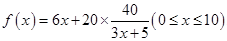 ;(Ⅱ)隔热层修建多厚时,总费用
;(Ⅱ)隔热层修建多厚时,总费用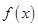 最小,并求最小值,由
最小,并求最小值,由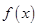 的解析式可知,
的解析式可知,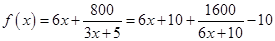 ,有基本不等式即可求出。
,有基本不等式即可求出。
试题解析:(Ⅰ)由题意,当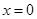 时,
时,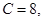 那么
那么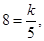 则
则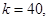 那么
那么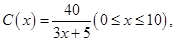
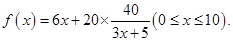
(Ⅱ)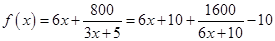
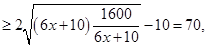
等号成立时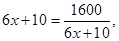 的
的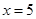 答:略.
答:略.
考点:应用题,基本不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目