题目内容
点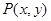 是曲线
是曲线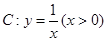 上的动点,曲线
上的动点,曲线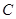 在点
在点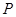 处的切线与
处的切线与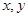 轴分别交于
轴分别交于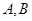 两点,点
两点,点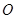 是坐标原点.给出三个结论:①
是坐标原点.给出三个结论:①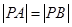 ;②△
;②△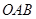 的周长有最小值
的周长有最小值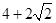 ;③曲线
;③曲线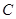 上存在两点
上存在两点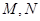 ,使得△
,使得△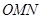 为等腰直角三角形.其中正确结论的个数是
为等腰直角三角形.其中正确结论的个数是
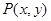 是曲线
是曲线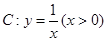 上的动点,曲线
上的动点,曲线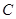 在点
在点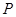 处的切线与
处的切线与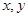 轴分别交于
轴分别交于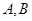 两点,点
两点,点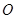 是坐标原点.给出三个结论:①
是坐标原点.给出三个结论:①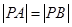 ;②△
;②△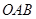 的周长有最小值
的周长有最小值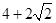 ;③曲线
;③曲线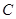 上存在两点
上存在两点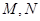 ,使得△
,使得△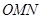 为等腰直角三角形.其中正确结论的个数是
为等腰直角三角形.其中正确结论的个数是| A.1 | B.2 | C.3 | D.0 |
C
试题分析:设动点P(m,
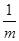 )(m>0),则y′=-
)(m>0),则y′=-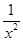 ,∴f′(m)=-
,∴f′(m)=-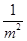 ,
,∴过动点P(m,
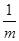 )的切线方程为:y-
)的切线方程为:y-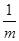 =-
=-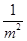 (x-m).
(x-m).①分别令y=0,x=0,得A(2m,0),B(0,
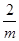 ).
).则|PA|=
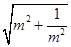 ,|PB|=
,|PB|=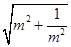 ,∴|PA|=|PB|,故①正确;
,∴|PA|=|PB|,故①正确;②由上面可知:△OAB的周长=2m+
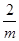 +2
+2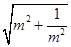 ≥2×2+2
≥2×2+2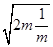 =4+2
=4+2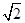 ,当且仅当m=
,当且仅当m=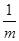 ,即m=1时取等号.故△OAB的周长有最小值4+2
,即m=1时取等号.故△OAB的周长有最小值4+2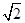 ,即②正确.
,即②正确.③假设曲线C上存在两点M(a,
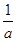 ),N(b,
),N(b,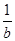 ),不妨设0<a<b,∠OMN=90°.
),不妨设0<a<b,∠OMN=90°.则|ON|=
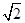 |OM|,
|OM|,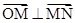 ,
,所以
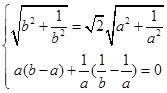
化为
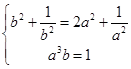 ,解得
,解得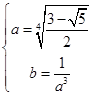 ,故假设成立.因此③正确.
,故假设成立.因此③正确.故选C。
点评:理解导数的几何意义、基本不等式的性质、两点间的距离公式及等腰直角三角形的性质是解题的关键.较难。

练习册系列答案
相关题目
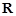 的函数
的函数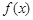 满足
满足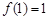 ,
,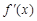 是
是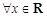
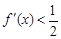 则不等式
则不等式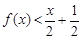 的解集为_______.
的解集为_______.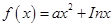 存在垂直于
存在垂直于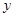 轴的切线,则实数
轴的切线,则实数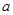 的取值范围是 。
的取值范围是 。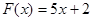 (
(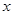 单位为
单位为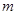 ,
,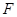 单位为
单位为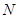 )的作用下,沿着与力
)的作用下,沿着与力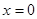 处运动到
处运动到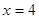 处,则力
处,则力
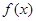 的单调性;
的单调性;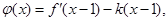 若函数
若函数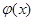 有两个零点
有两个零点 ,求证
,求证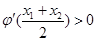
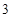
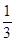
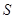 (米)与时间
(米)与时间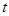 (秒)的关系是
(秒)的关系是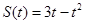 ,则物体在
,则物体在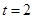 秒时的瞬时速度为( )
秒时的瞬时速度为( ) m/s
m/s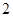 m/s
m/s m/s
m/s m/s
m/s 上的函数
上的函数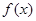 满足
满足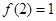 ,且
,且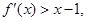 则不等式
则不等式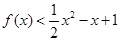 的解集为( )
的解集为( )

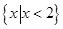
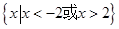
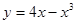 在点(-1,-3)处的切线方程是
在点(-1,-3)处的切线方程是